【題目】已知四棱錐
中，側(cè)面
底面
，
，
是邊長為2的正三角形底面是菱形，點(diǎn)
為
的中點(diǎn)
（1）求證：
平面
；
（2）求二面角
的余弦值.
【答案】（1）見解析；（2）
【解析】
(1) 連結(jié)AC，交BD于O，利用中位線定理證明
，結(jié)合線面平行的判定定理證明即可；
(2)建立空間直角坐標(biāo)系，利用坐標(biāo)求出平面PAB和平面PBC的法向量，即可求解.
（1）
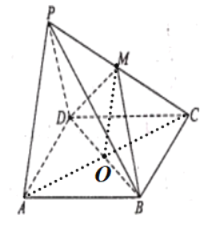
連結(jié)AC，交BD于O，連接MO，由于底面ABCD為菱形，
O為AC中點(diǎn)
又M為
的中點(diǎn)，，又
面
，
面
平面
（2）過
作
，垂足為
，由于
為正三角形，為
的中點(diǎn)．由于側(cè)面
面
，由面面垂直的性質(zhì)得
面，
由
，得
∴
以E為坐標(biāo)原點(diǎn)，EP為
軸，EA為
軸，EB為y軸，建立空間直角坐標(biāo)系．
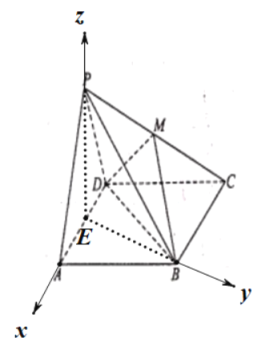
則
，
設(shè)平面PAB的法向量為
，平面PBC的法向量為
由
及
得
，取
，得平面PAB的一個法向量為
同理可求得平面PBC的一個法向量
，由法向量的方向得知
所求二面角的余弦值為
.
新課標(biāo)階梯閱讀訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在直角坐標(biāo)系
中，長為3的線段的兩端點(diǎn)
分別在
軸、
軸上滑動，點(diǎn)
為線段
上的點(diǎn)，且滿足
.記點(diǎn)的軌跡為曲線
.
（1）求曲線的方程；
（2）若點(diǎn)
為曲線上的兩個動點(diǎn)，記
，判斷是否存在常數(shù)
使得點(diǎn)
到直線
的距離為定值？若存在，求出常數(shù)的值和這個定值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
中心在坐標(biāo)原點(diǎn)，焦點(diǎn)在
軸上，且過點(diǎn)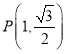
，直線
與橢圓交于
兩點(diǎn)（兩點(diǎn)不是左右頂點(diǎn)），若直線的斜率為
時，弦
的中點(diǎn)
在直線
上.
（1）求橢圓的方程；
（2）若在橢圓上有相異的兩點(diǎn)（
三點(diǎn)不共線），
為坐標(biāo)原點(diǎn)，且直線，直線
，直線
的斜率滿足
，求證：
是定值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】給出下列五個命題，其中正確命題的個數(shù)為（ ）
①命題“
，使得
”的否定是“
，均有
”；
②若正整數(shù)
和
滿足
，則
；
③在
中 ，
是
的充要條件；
④一條光線經(jīng)過點(diǎn)
，射在直線
上，反射后穿過點(diǎn)
，則入射光線所在直線的方程為
；
⑤已知
的三個零點(diǎn)分別為一橢圓、一雙曲線、一拋物線的離心率，則
為定值.
A.2B.3C.4D.5
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．若g（x）存在2個零點(diǎn)，則a的取值范圍是
A. [–1，0） B. [0，+∞） C. [–1，+∞） D. [1，+∞）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
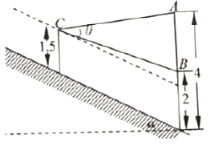
【題目】如圖，一幅壁畫的最高點(diǎn)
處離地面
米，最低點(diǎn)
處離地面
米.正對壁畫的是一條坡度為
的甬道（坡度指斜坡與水平面所成角
的正切值），若從離斜坡地面
米的
處觀賞它.
（1）若對墻的投影（即過作
的垂線垂足為投影）恰在線段（包括端點(diǎn)）上，求點(diǎn)離墻的水平距離的范圍；
（2）在（1）的條件下，當(dāng)點(diǎn)離墻的水平距離為多少時，視角
（
）最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
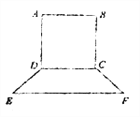
【題目】要制作一個如圖的框架（單位：米）.要求所圍成的總面積為19.5（
），其中
是一個矩形， 
是一個等腰梯形，梯形高
， 
，設(shè)
米， 
米.
（1）求
關(guān)于
的表達(dá)式；
（2）如何設(shè)計，的長度，才能使所用材料最少？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知如圖1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D為AC中點(diǎn)，AE
BD于E，延長AE交BC于F，將△ABD沿BD折起，使平面ABD平面BCD，如圖2所示。
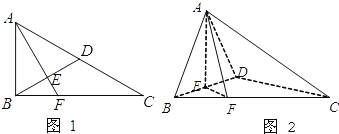
（Ⅰ）求證：AE平面BCD；
（Ⅱ）求二面角A-DC-B的余弦值；
（Ⅲ）求三棱錐B-AEF與四棱錐A-FEDC的體積的比（只需寫出結(jié)果，不要求過程）．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com