
【題目】如圖所示,正方體ABCD﹣A1B1C1D1的棱長為1,BD∩AC=0,M是線段D1O上的動點,過點M做平面ACD1的垂線交平面A1B1C1D1于點N,則點N到點A距離的最小值為( ) 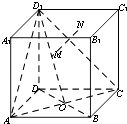
A.![]()
B.![]()
C.![]()
D.1
 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和記為
項和記為![]() ,
, ![]() ,點
,點![]() 在直線
在直線![]() 上,其中
上,其中![]() .
.
(1)若數列![]() 是等比數列,求實數
是等比數列,求實數![]() 的值;
的值;
(2)設各項均不為0的數列![]() 中,所有滿足
中,所有滿足![]() 的整數
的整數![]() 的個數稱為這個數列
的個數稱為這個數列![]() 的“積異號數”,令
的“積異號數”,令![]() (
(![]() ),在(1)的條件下,求數列
),在(1)的條件下,求數列![]() 的“積異號數”.
的“積異號數”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2015江蘇高考,18】如圖,在平面直角坐標系xOy中,已知橢圓![]() 的離心率為
的離心率為![]() ,且右焦點F到左準線l的距離為3.
,且右焦點F到左準線l的距離為3.
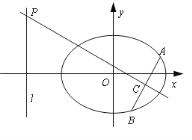
(1)求橢圓的標準方程;
(2)過F的直線與橢圓交于A,B兩點,線段AB的垂直平分線分別交直線l和AB于點P,C,若PC=2AB,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在D上的函數,若存在區間[m,n]D及正實數k,使函數f(x)在[m,n]上的值域恰為[km,kn],則稱函數f(x)是k型函數.給出下列說法:
①f(x)=3﹣ ![]() 不可能是k型函數;
不可能是k型函數;
②若函數f(x)= ![]() (a≠0)是1型函數,則n﹣m的最大值為
(a≠0)是1型函數,則n﹣m的最大值為 ![]() ;
;
③若函數f(x)=﹣ ![]() x2+x是3型函數,則m=﹣4,n=0.
x2+x是3型函數,則m=﹣4,n=0.
其中正確說法個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx,其中ω>0,若f(x)相鄰兩條對稱軸間的距離不小于
cosωxsinωx,其中ω>0,若f(x)相鄰兩條對稱軸間的距離不小于 ![]()
(1)求ω的取值范圍及函數f(x)的單調遞增區間;
(2)在△ABC中,a,b,c分別是角A,B,C的對邊,a= ![]() ,b+c=3,當ω最大時,f(A)=1,求sinBsinC的值.
,b+c=3,當ω最大時,f(A)=1,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() .
.
(1)若f(x)>k的解集為{x|x<﹣3或x>﹣2},求k的值;
(2)若對任意x>0,f(x)≤t恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市對貧困家庭自主創業給予小額貸款補貼,每戶貸款額為![]() 萬元,貸款期限有
萬元,貸款期限有![]() 個月、
個月、![]() 個月、
個月、![]() 個月、
個月、![]() 個月、
個月、![]() 個月五種,這五種貸款期限政府分別需要補助
個月五種,這五種貸款期限政府分別需要補助![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元,從
元,從![]() 年享受此項政策的困難戶中抽取了
年享受此項政策的困難戶中抽取了![]() 戶進行了調查統計,選取貸款期限的頻數如下表:
戶進行了調查統計,選取貸款期限的頻數如下表:
貸款期限 |
|
|
|
|
|
頻數 |
|
|
|
|
|
以商標各種貸款期限的頻率作為![]() 年貧困家庭選擇各種貸款期限的概率.
年貧困家庭選擇各種貸款期限的概率.
(1)某小區![]() 年共有
年共有![]() 戶準備享受此項政策,計算其中恰有兩戶選擇貸款期限為
戶準備享受此項政策,計算其中恰有兩戶選擇貸款期限為![]() 個月的概率;
個月的概率;
(2)設給享受此項政策的某困難戶補貼為![]() 元,寫出
元,寫出![]() 的分布列,若預計
的分布列,若預計![]() 年全市有
年全市有![]() 萬戶享受此項政策,估計
萬戶享受此項政策,估計![]() 年該市共要補貼多少萬元.
年該市共要補貼多少萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com