分析:將函數的解析式化為根式,進而根據使函數解析式有意義的原則求出函數的定義域,可判斷①;
利用分離常數法和分析法,求出函數f(x)=
(x>0)的值域,可判斷②;
分析函數的定義域是否關于原點對稱,并判斷f(-x)+f(x)=0是否成立,進而根據奇函數的定義,可判斷③;
利用平方法,根據3
x+3
-x=2
,求出(3
x-3
-x)
2=4,但由于3
x與3
-x的大小不確定,故3
x-3
-x=±2,可判斷④.
解答:解:函數y=x
-=
,要使函數的解析式有意義,自變量須滿足x>0,故函數y=x
-的定義域是{x|x>0},故①錯誤;
函數f(x)=
=2+
,當x>0時,0<
<1,故2+
∈(2,3),故②函數f(x)=
(x>0)的值域是(2,3)正確;
函數y=f(x)=lg
的定義域為(-1,1)關于原點對稱,則f(-x)+f(x)=lg
+lg
=lg(
•
)=lg1=0,故函數③函數y=lg
在定義域上為奇函數正確;
若3
x+3
-x=2
,故(3
x+3
-x)
2=3
2x+3
-2x+2=8,故3
2x+3
-2x=6;故(3
x-3
-x)
2=3
2x+3
-2x-2=4,故3
x-3
-x=±2,故④錯誤
故答案為:②③
點評:本題考查的知識點是對數函數的圖象和性質,函數的奇偶性的定義,有理數指數冪與根式,函數的定義域,是函數圖象和性質的綜合應用,難度中檔.



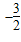 的定義域是{x|x≠0};
的定義域是{x|x≠0};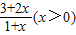 的值域是(2,3);
的值域是(2,3);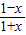 在定義域上為奇函數;
在定義域上為奇函數;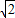 ,則3x-3-x的值為2.
,則3x-3-x的值為2.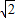 .
.