
【題目】已知![]() ,函數
,函數![]() ,直線
,直線![]() .
.
![]() 討論
討論![]() 的圖象與直線
的圖象與直線![]() 的交點個數;
的交點個數;
![]() 若函數
若函數![]() 的圖象與直線
的圖象與直線![]() 相交于
相交于![]() ,
,![]() 兩點
兩點![]() ,證明:
,證明:![]() .
.
【答案】(1)當![]() 時,
時,![]() 無交點;
無交點;![]() 時,
時,![]() 有一個交點;
有一個交點;![]() 時,
時,![]() 有兩個交點;(2)證明見解析.
有兩個交點;(2)證明見解析.
【解析】
![]() 根據函數與方程的關系,設
根據函數與方程的關系,設![]() ,求函數的導數,研究函數的單調性和極值,結合極值與0的關系進行判斷即可.
,求函數的導數,研究函數的單調性和極值,結合極值與0的關系進行判斷即可.
![]() 構造函數
構造函數![]() ,求函數的導數,結合
,求函數的導數,結合![]() 與l的交點坐標,進行證明即可.
與l的交點坐標,進行證明即可.
![]() 由題意,令
由題意,令![]() ,
,![]()
則![]() ,
,
令![]() ,解得
,解得![]() .
.
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
令![]() ,解得
,解得![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,
則當![]() 時,函數取得極小值,同時也是最小值
時,函數取得極小值,同時也是最小值
![]() .
.
![]() 當
當![]() ,即
,即![]() 時,
時,![]() 的圖象與直線l無交點,
的圖象與直線l無交點,
![]() 當
當![]() ,即
,即![]() 時
時![]() 的圖象與直線l只有一個交點.
的圖象與直線l只有一個交點.
![]() 當
當![]() ,即
,即![]() 時
時![]() 的圖象與直線l有兩個交點.
的圖象與直線l有兩個交點.
綜上所述,當![]() 時,
時,![]() 的圖象與直線l無交點;
的圖象與直線l無交點;![]() 時,
時,![]() 的圖象與直線l只有一個交點;
的圖象與直線l只有一個交點;![]() 時
時![]() 的圖象與直線l有兩個交點.
的圖象與直線l有兩個交點.
![]() 證明:令
證明:令![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
![]() 時,
時,![]() 恒成立,
恒成立,
又![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
又![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() 即
即![]() .
.
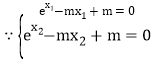 ,
,
![]() ,
,
![]() .
.
![]() ,
,
即![]() ,則
,則![]() ,
,
![]() ,
,
即![]() ,
,
即![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】如圖,GH是東西方向的公路北側的邊緣線,某公司準備在GH上的一點B的正北方向的A處建設一倉庫,設![]() ,并在公路北側建造邊長為
,并在公路北側建造邊長為![]() 的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且
的正方形無頂中轉站CDEF(其中EF在GH上),現從倉庫A向GH和中轉站分別修兩條道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 關于
關于![]() 的函數解析式,并求出定義域;
的函數解析式,并求出定義域;
(2)如果中轉站四堵圍墻造價為10萬元/km,兩條道路造價為30萬元/km,問:![]() 取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.
取何值時,該公司建設中轉站圍墻和兩條道路總造價M最低.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,圓C的方程為ρ=4cosθ,以極點為坐標原點,極軸為x軸的非負半軸建立平面直角坐標系,直線l經過點M(5,6),且斜率為![]() .
.
(1)求圓 C的平面直角坐標方程和直線l的參數方程;
(2)若直線l與圓C交于A,B兩點,求|MA|+|MB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工企業2018年年底投入100萬元,購入一套污水處理設備。該設備每年的運轉費用是0.5萬元,此外,每年都要花費一定的維護費,第一年的維護費為2萬元,由于設備老化,以后每年的維護費都比上一年增加2萬元。設該企業使用該設備![]() 年的年平均污水處理費用為
年的年平均污水處理費用為![]() (單位:萬元)
(單位:萬元)
(1)用![]() 表示
表示![]() ;
;
(2)當該企業的年平均污水處理費用最低時,企業需重新更換新的污水處理設備。則該企業幾年后需要重新更換新的污水處理設備。
查看答案和解析>>
科目:高中數學 來源: 題型:
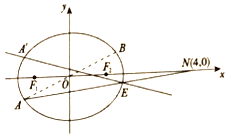
【題目】如圖,已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,
上任意一點,![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,有
,有![]() ,且
,且![]() 的最大值
的最大值![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 是
是![]() 關于
關于![]() 軸的對稱點,設點
軸的對稱點,設點![]() ,連接
,連接![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小學舉辦“父母養育我,我報父母恩”的活動,對六個年級(一年級到六年級的年級代碼分別為1,2…,6)的學生給父母洗腳的百分比y%進行了調查統計,繪制得到下面的散點圖.
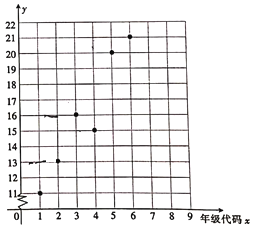
(1)由散點圖看出,可用線性回歸模型擬合y與x的關系,請用相關系數加以說明;
(2)建立y關于x的回歸方程,并據此預計該校學生升入中學的第一年(年級代碼為7)給父母洗腳的百分比.
附注:參考數據:![]()
參考公式:相關系數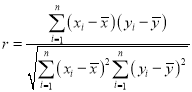 ,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程
,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程![]() 中斜率與截距的最小二乘估計公式分別為
中斜率與截距的最小二乘估計公式分別為![]() =
=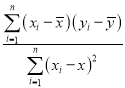 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com