
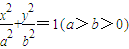 ,左頂點A(
,左頂點A(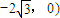 ,AC⊥CO,|AC|=|CO|.a2=12,C(
,AC⊥CO,|AC|=|CO|.a2=12,C(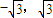 )再由C在橢圓上知b2=4,由此能導出橢圓的標準方程.
)再由C在橢圓上知b2=4,由此能導出橢圓的標準方程.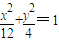 得4x2-6mx+3m2-12=0,由題設條件能導出|MN|=
得4x2-6mx+3m2-12=0,由題設條件能導出|MN|=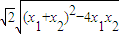 =
=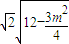 ,又C到直線l的距離d=
,又C到直線l的距離d=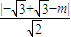 =
=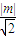 ,所以△CMN的面積S=
,所以△CMN的面積S=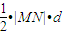 =
=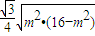
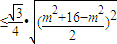 =2
=2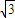 ,由此能求出直線l的方程.
,由此能求出直線l的方程.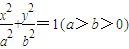 ,
,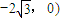 ,AC⊥CO,|AC|=|CO|.
,AC⊥CO,|AC|=|CO|.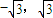 ),(第三象限的點相同,可以不考慮)(2分)
),(第三象限的點相同,可以不考慮)(2分)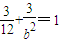 ,∴b2=4,(4分)
,∴b2=4,(4分)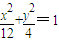 .(5分)
.(5分)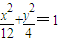 得4x2-6mx+3m2-12=0,(6分)
得4x2-6mx+3m2-12=0,(6分)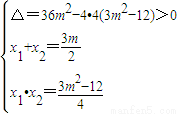 (7分)
(7分)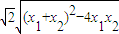 =
=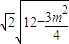 ,(8分)
,(8分)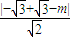 =
=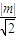 ,(9分)
,(9分)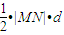 =
=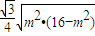 (10分)
(10分)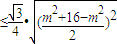 =2
=2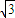 ,(11分)
,(11分)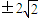 滿足題中條件,(12分)
滿足題中條件,(12分)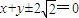 .(13分)
.(13分)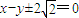 (14分)
(14分)

科目:高中數學 來源: 題型:
| ||
| 2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 25 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com