
【題目】已知F1 , F2分別是橢圓C: ![]() (a>b>0)的兩個焦點,P(1,
(a>b>0)的兩個焦點,P(1, ![]() )是橢圓上一點,且
)是橢圓上一點,且 ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差數列.
|PF2|成等差數列.
(1)求橢圓C的標準方程;
(2)已知動直線l過點F2 , 且與橢圓C交于A,B兩點,試問x軸上是否存在定點Q,使得 ![]()
![]() =﹣
=﹣ ![]() 恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
【答案】
(1)解:∵ ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差數列,
|PF2|成等差數列,
∴ ![]() |PF1|+
|PF1|+ ![]() |PF2|=2|F1F2|,即2
|PF2|=2|F1F2|,即2 ![]() a=4c,∴a=
a=4c,∴a= ![]() c.
c.
∴ 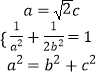 ,解得
,解得 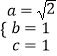 .
.
∴橢圓方程為 ![]()
(2)解:假設在x軸上存在點Q(m,0),使得 ![]() 恒成立.
恒成立.
①當直線l的斜率為0時,A(﹣ ![]() ,0),B(
,0),B( ![]() ,0).
,0).
∴ ![]() =(﹣
=(﹣ ![]() ﹣m,0),
﹣m,0), ![]() =(
=( ![]() ﹣m,0).
﹣m,0).
∴ ![]() =m2﹣2=﹣
=m2﹣2=﹣ ![]() ,解得
,解得 ![]() 或m=﹣
或m=﹣ ![]() .
.
②若直線l斜率不為0,設直線AB的方程為x=ty+1.
聯立方程組 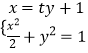 ,消元得:(t2+2)y2+2ty﹣1=0.
,消元得:(t2+2)y2+2ty﹣1=0.
設A(x1,y1),B(x2,y2),則y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() .
.
∴x1+x2=t(y1+y2)+2= ![]() ,
,
x1x2=(ty1+1)(ty2+1)=t2y1y2+t(y1+y2)+1= ![]() .
.
∵ ![]() =(x1﹣m,y1),
=(x1﹣m,y1), ![]() =(x2﹣m,y2).
=(x2﹣m,y2).
∴ ![]() =(x1﹣m)(x2﹣m)+y1y2=x1x2﹣m(x1+x2)+m2+y1y2
=(x1﹣m)(x2﹣m)+y1y2=x1x2﹣m(x1+x2)+m2+y1y2
= ![]() ﹣
﹣ ![]() +m2﹣
+m2﹣ ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴ 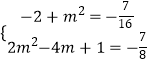 ,解得m=
,解得m= ![]() .
.
綜上,Q點坐標為( ![]() ,0)
,0)
【解析】


科目:高中數學 來源: 題型:
【題目】各項均為正數的數列{bn}的前n項和為Sn , 且對任意正整數n,都有2Sn=bn(bn+1).
(1)求數列{bn}的通項公式;
(2)如果等比數列{an}共有2015項,其首項與公比均為2,在數列{an}的每相鄰兩項ak與ak+1之間插入k個(﹣1)kbk(k∈N*)后,得到一個新的數列{cn}.求數列{cn}中所有項的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,求實數λ的范圍.
成立,求實數λ的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點C為圓(x+1)2+y2=8的圓心,P是圓上的動點,點Q在圓的半徑CP上,且有點A(1,0)和AP上的點M,滿足 ![]()
![]() =0,
=0, ![]() =2
=2 ![]() .
.
(1)當點P在圓上運動時,求點Q的軌跡方程;
(2)若斜率為k的直線 l與圓x2+y2=1相切,直線 l與(1)中所求點Q的軌跡交于不同的兩點F,H,O是坐標原點,且 ![]() ≤
≤ ![]()
![]() ≤
≤ ![]() 時,求k的取值范圍.
時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設D是函數y=f(x)定義域內的一個區間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數API的監測數據,結果統計如下:
API | [0,100] | (100,200] | (200,300] | >300 |
空氣質量 | 優良 | 輕污染 | 中度污染 | 重度污染 |
天數 | 17 | 45 | 18 | 20 |
記某企業每天由空氣污染造成的經濟損失S(單位:元),空氣質量指數API為![]() .當
.當![]() 時,企業沒有造成經濟損失;當
時,企業沒有造成經濟損失;當![]() 對企業造成經濟損失成直線模型(當
對企業造成經濟損失成直線模型(當![]() 時造成的經濟損失為
時造成的經濟損失為![]() ,當
,當![]() 時,造成的經濟損失
時,造成的經濟損失![]() );當
);當![]() 時造成的經濟損失為2000元;
時造成的經濟損失為2000元;
(1)試寫出![]() 的表達式;
的表達式;
(2)若本次抽取的樣本數據有30天是在供暖季,其中有12天為重度污染,完成下面2×2列聯表,并判斷能否有99%的把握認為該市本年空氣重度污染與供暖有關?
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
![]()
P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市理論預測2010年到2014年人口總數與年份的關系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口數y(十萬) | 5 | 7 | 8 | 11 | 19 |
(1)請根據上表提供的數據,求出y關于x的線性回歸方程;
(2) 據此估計2015年該城市人口總數。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某跳水運動員在一次跳水訓練時的跳水曲線為如圖所示拋物線的一段.已知跳水板![]() 長為
長為![]() ,跳水板距水面
,跳水板距水面![]() 的高
的高![]() 為
為![]() .為安全和空中姿態優美,訓練時跳水曲線應在離起跳點
.為安全和空中姿態優美,訓練時跳水曲線應在離起跳點![]() 處水平距
處水平距![]()
![]() 時達到距水面最大高度
時達到距水面最大高度![]() ,規定:以
,規定:以![]() 為橫軸,
為橫軸,![]() 為縱軸建立直角坐標系.
為縱軸建立直角坐標系.
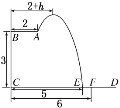
(1)當![]() 時,求跳水曲線所在的拋物線方程;
時,求跳水曲線所在的拋物線方程;
(2)若跳水運動員在區域![]() 內入水時才能達到比較好的訓練效果,求此時
內入水時才能達到比較好的訓練效果,求此時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sin(x+ ![]() )的圖象上各點的橫坐標壓縮為原來的
)的圖象上各點的橫坐標壓縮為原來的 ![]() 倍(縱坐標不變),所得函數在下面哪個區間單調遞增( )
倍(縱坐標不變),所得函數在下面哪個區間單調遞增( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com