
【題目】已知以橢圓![]() 的焦點和短軸端點為頂點的四邊形恰好是面積為4的正方形.
的焦點和短軸端點為頂點的四邊形恰好是面積為4的正方形.
(1)求橢圓![]() 的方程:
的方程:
(2)若![]() 是橢圓
是橢圓![]() 上的動點,求
上的動點,求![]() 的取值范圍;
的取值范圍;
(3)直線![]() :
:![]() 與橢圓
與橢圓![]() 交于異于橢圓頂點的
交于異于橢圓頂點的![]() ,
,![]() 兩點,
兩點,![]() 為坐標原點,直線
為坐標原點,直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() 點,直線
點,直線![]() 和直線
和直線![]() 的斜率之積為1,直線
的斜率之積為1,直線![]() 與
與![]() 軸交于點
軸交于點![]() .若直線
.若直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() 試判斷
試判斷![]() ,是否為定值,若是,求出該定值;若不是,說明理由.
,是否為定值,若是,求出該定值;若不是,說明理由.
 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】已知命題![]() :
: ![]() 表示雙曲線,命題
表示雙曲線,命題![]() :
: ![]() 表示橢圓。
表示橢圓。
(1)若命題![]() 與命題
與命題![]() 都為真命題,則
都為真命題,則![]() 是
是![]() 的什么條件?
的什么條件?
(請用簡要過程說明是“充分不必要條件”、“必要不充分條件”、“充要條件”和“既不充分也不必要條件”中的哪一個)
(2)若![]() 為假命題,且
為假命題,且![]() 為真命題,求實數
為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為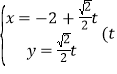 為參數
為參數![]() ,直線
,直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)若點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形周長的最大值.
的內接矩形周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,動點![]() 分別與兩個定點
分別與兩個定點![]() ,
,![]() 的連線的斜率之積為
的連線的斜率之積為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設過點![]() 的直線與軌跡
的直線與軌跡![]() 交于
交于![]() ,
,![]() 兩點,判斷直線
兩點,判斷直線![]() 與以線段
與以線段![]() 為直徑的圓的位置關系,并說明理由.
為直徑的圓的位置關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱錐D-ABC中,二面角A-BC-D的大小為90°,且∠BDC=90°,∠ABC=30°,BC=3,![]() .
.
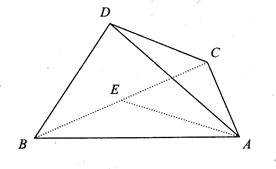
(1)求證:AC⊥平面BCD;
(2)二面角B-AC-D為45°,且E為線段BC的中點,求直線AE與平面ACD所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如下表(假設該區域空氣質量指數不會超過300):
空氣質量指數 |
|
|
|
|
|
|
空氣質量等級 | 1級優 | 2級良 | 3級輕度污染 | 4級中度污染 | 5級重度污染 | 6級嚴重污染 |
該社團將該校區在2018年11月中10天的空氣質量指數監測數據作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
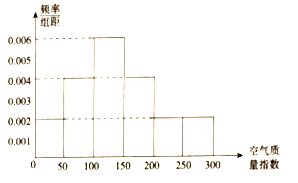
(1)以這10天的空氣質量指數監測數據作為估計2018年11月的空氣質量情況,則2018年11月中有多少天的空氣質量達到優良?
(2)從這10天的空氣質量指數監測數據中,隨機抽取三天,求恰好有一天空氣質量良的概率;
(3)從這10天的數據中任取三天數據,記![]() 表示抽取空氣質量良的天數,求
表示抽取空氣質量良的天數,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com