已知數(shù)列{a
n}滿足:a
1=

,a
2=

,a
n+1=2a
n-a
n-1(n≥2,n∈N
*),數(shù)列{b
n}滿足b
1<0,3b
n-b
n-1=n(n≥2,n∈N
*),數(shù)列{b
n}的前n項和為S
n.
(1)求數(shù)列{a
n}的通項a
n.
(2)求證:數(shù)列{b
n-a
n}為等比數(shù)列.
【答案】
分析:(1)2a
n=a
n+1+a
n-1,根據(jù)等差數(shù)列的定義可知∴{a
n}是等差數(shù)列.根據(jù)a
1和a
2,求得公差,則數(shù)列{a
n}的通項a
n可得.
(2)把a
n和b
n代入b
n+1-a
n+1進而化簡整理b
n+1-a
n+1=

(b
n-a
n),進而可判斷∴{b
n-a
n}是以b
1-

為首項,以

為公比的等比數(shù)列.
解答:解:(1)證明∵2a
n=a
n+1+a
n-1(n≥2,n∈N
*),
∴a
n+1-a
n=a
n-a
n-1∴{a
n}是等差數(shù)列.
又∵a
1=

,a
2=

,∴a
n=

+(n-1)•

=
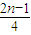
,
(2)證明:∵b
n=

b
n-1+
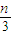
(n≥2,n∈N
*),
∴b
n+1-a
n+1=

b
n+
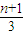
-
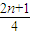
=

b
n-
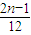
=

(b
n-

)=

(b
n-a
n).
又∵b
1-a
1=b
1-

≠0,
∴{b
n-a
n}是以b
1-

為首項,以

為公比的等比數(shù)列.
點評:本題主要考查了等差數(shù)列的通項公式和等比關(guān)系的確定.考查了學(xué)生綜合把握數(shù)列基礎(chǔ)知識.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
已知數(shù)列{a
n}滿足:a
1=1且
an+1=, n∈N*.
(1)若數(shù)列{b
n}滿足:
bn=(n∈N*),試證明數(shù)列b
n-1是等比數(shù)列;
(2)求數(shù)列{a
nb
n}的前n項和S
n;
(3)數(shù)列{a
n-b
n}是否存在最大項,如果存在求出,若不存在說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知數(shù)列{a
n}滿足
a1+a2+a3+…+an=2n+1則{a
n}的通項公式
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知數(shù)列{a
n}滿足:a
1=
,且a
n=
(n≥2,n∈N
*).
(1)求數(shù)列{a
n}的通項公式;
(2)證明:對于一切正整數(shù)n,不等式a
1•a
2•…a
n<2•n!
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知數(shù)列{a
n}滿足a
n+1=|a
n-1|(n∈N
*)
(1)若
a1=,求a
n;
(2)若a
1=a∈(k,k+1),(k∈N
*),求{a
n}的前3k項的和S
3k(用k,a表示)
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
(2012•北京模擬)已知數(shù)列{a
n}滿足a
n+1=a
n+2,且a
1=1,那么它的通項公式a
n等于
2n-1
2n-1
.
查看答案和解析>>

 ,a2=
,a2= ,an+1=2an-an-1(n≥2,n∈N*),數(shù)列{bn}滿足b1<0,3bn-bn-1=n(n≥2,n∈N*),數(shù)列{bn}的前n項和為Sn.
,an+1=2an-an-1(n≥2,n∈N*),數(shù)列{bn}滿足b1<0,3bn-bn-1=n(n≥2,n∈N*),數(shù)列{bn}的前n項和為Sn. (bn-an),進而可判斷∴{bn-an}是以b1-
(bn-an),進而可判斷∴{bn-an}是以b1- 為首項,以
為首項,以 為公比的等比數(shù)列.
為公比的等比數(shù)列. ,a2=
,a2= ,∴an=
,∴an= +(n-1)•
+(n-1)• =
=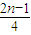 ,
, bn-1+
bn-1+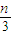 (n≥2,n∈N*),
(n≥2,n∈N*), bn+
bn+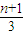 -
-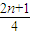 =
= bn-
bn-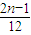
 (bn-
(bn- )=
)= (bn-an).
(bn-an). ≠0,
≠0, 為首項,以
為首項,以 為公比的等比數(shù)列.
為公比的等比數(shù)列.

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案