
若函數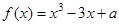 有三個不同的零點,則實數
有三個不同的零點,則實數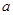 的取值范圍是 .
的取值范圍是 .
(-2,2)
【解析】
試題分析:解:由函數 有三個不同的零點,
有三個不同的零點,
則函數f(x)有兩個極值點,極小值小于0,極大值大于0;
由f′(x)=3x2-3=3(x+1)(x-1)=0,解得x1=1,x2=-1,
所以函數f(x)的兩個極,x∈(-∞,-1),f′(x)>0,x∈(-1,1),f′(x)<0,
x∈(1,+∞),f′(x)>0,
∴函數的極小值f(1)=a-2和極大值f(-1)=a+2.
因為函數f(x)=x3-3x+a有三個不同的零點,
所以a+2>0,a-2<0,,解之,得-2<a<2.
故實數a的取值范圍是(-2,2).
考點:運用導數研究函數的極值
點評:本題是中檔題,考查函數的導數與函數的極值的關系,考查轉化思想,計算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
|
| π |
| 3 |
1+
| ||
| 4 |
1+
| ||
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2014屆四川省高二“零診”考試文科數學試卷(解析版) 題型:解答題
已知函數 (其中a,b為實常數)。
(其中a,b為實常數)。
(Ⅰ)討論函數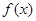 的單調區間:
的單調區間:
(Ⅱ)當 時,函數
時,函數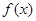 有三個不同的零點,證明:
有三個不同的零點,證明: :
:
(Ⅲ)若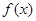 在區間
在區間 上是減函數,設關于x的方程
上是減函數,設關于x的方程 的兩個非零實數根為
的兩個非零實數根為 ,
, 。試問是否存在實數m,使得
。試問是否存在實數m,使得 對任意滿足條件的a及t
對任意滿足條件的a及t 恒成立?若存在,求m的取值范圍;若不存在,請說明理由。
恒成立?若存在,求m的取值范圍;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市黃浦區高三上學期期終基礎學業測評理科數學試卷 題型:填空題
(理科)已知函數
 是非零常數,關于
是非零常數,關于 的方程
的方程 有且僅有三個不同的實數根,若
有且僅有三個不同的實數根,若 分別是三個根中的最小根和最大根,則
分別是三個根中的最小根和最大根,則 =
.
=
.
查看答案和解析>>
科目:高中數學 來源:2012年上海市黃浦區高考數學一模試卷(理科)(解析版) 題型:解答題
 ,M是非零常數,關于X的方程f(x)=m(m∈R)有且僅有三個不同的實數根,若b、a分別是三個根中的最小根和最大根,則
,M是非零常數,關于X的方程f(x)=m(m∈R)有且僅有三個不同的實數根,若b、a分別是三個根中的最小根和最大根,則 = .
= .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com