【題目】已知函數
.
（1）當
時，求
的單調區間；
（2）若函數有兩個極值點
，
，且
，
為的導函數，設
，求
的取值范圍，并求取到最小值時所對應的
的值.
【答案】（1）單調遞增區間為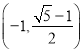
，單調遞減區間為
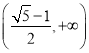（2）
的取值范圍是
；對應的
的值為
.
【解析】
（1）當
時，求
的導數可得函數的單調區間；（2）若函數有兩個極值點
，
，且
，利用導函數
，可得的范圍，再表達
，構造新函數可求的取值范圍，從而可求取到最小值時所對應的的值．
（1）函數
由條件得函數的定義域：
，
當時，
，
所以：
，
時，
，
當
時，
，當
，
時，
，
則函數的單調增區間為：
，單調遞減區間為：
，；
（2）由條件得：
，，
由條件得
有兩根：，，滿足
，
△
，可得：
或
；
由
，可得：
．
，
函數
的對稱軸為
，，
所以：
，
；
，可得：
，
，
，則：
，
所以：
；
所以：
，
令
，
，
，
則
，
因為：
時，
，所以：
在
，
上是單調遞減，在
，上單調遞增，
因為：
，
（1）
，
，
（1），
所以
，
；
即的取值范圍是：
，；
，所以有
，
則
，
；
所以當取到最小值時所對應的的值為；
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知曲線
：
和
：
（
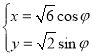為參數）.以原點
為極點，
軸的正半軸為極軸，建立極坐標系，且兩種坐標系中取相同的長度單位.
（1）求曲線的直角坐標方程和的方程化為極坐標方程；
（2）設與，
軸交于
，
兩點，且線段
的中點為
.若射線
與，交于，
兩點，求，兩點間的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖，90后從事互聯網行業崗位分布條形圖，則下列結論中不正確的是（ ）
注：90后指1990年及以后出生，80后指1980-1989年之間出生，80前指1979年及以前出生.
A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
（
）的左焦點為
，
是上一點，且
與
軸垂直，
，
分別為橢圓的右頂點和上頂點，且
，且
的面積是
，其中
是坐標原點.
（1）求橢圓的方程.
（2）若過點的直線
，
互相垂直，且分別與橢圓交于點
，
，
，
四點，求四邊形
的面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為F1，F2，過點F1的直線與C交于A，B兩點.△ABF2的周長為
，且橢圓的離心率為
.
（1）求橢圓C的標準方程：
（2）設點P為橢圓C的下頂點，直線PA，PB與y＝2分別交于點M，N，當|MN|最小時，求直線AB的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
