
【題目】已知![]() 是定義在R上的偶函數,當
是定義在R上的偶函數,當![]() 時,
時, ![]() .
.
(1)求![]() 的解析式;并畫出簡圖;
的解析式;并畫出簡圖;

(2)利用圖象討論方程![]() 的根的情況。(只需寫出結果,不要解答過程).
的根的情況。(只需寫出結果,不要解答過程).
(3)若直線![]() 與函數
與函數![]() 的圖像自左向右依次交于四個不同點 A,B,C,D .若AB=BC,求實數k的值.
的圖像自左向右依次交于四個不同點 A,B,C,D .若AB=BC,求實數k的值.
【答案】(1)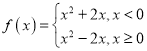 ,圖象見解析;(2)見解析;(3)
,圖象見解析;(2)見解析;(3)![]() .
.
【解析】
(1)利用偶函數的定義,可以求出當![]() 時,
時,![]() 的解析式,即可寫出
的解析式,即可寫出![]() 在R上的解析式,作出函數
在R上的解析式,作出函數![]() 在當
在當![]() 時的圖象,再根據偶函數關于
時的圖象,再根據偶函數關于![]() 軸對稱,即可畫出;
軸對稱,即可畫出;
(2)根據圖象即可觀察出方程![]() 的根的情況;
的根的情況;
(3)由圖象的對稱性,可知點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,點
對稱,點![]() 與點
與點![]() 關于
關于![]() 軸對稱,設出點
軸對稱,設出點![]() 的坐標,求出其它點的坐標,列出等式,求解即可.
的坐標,求出其它點的坐標,列出等式,求解即可.
(1)因為![]() 是定義在R上的偶函數,當
是定義在R上的偶函數,當![]() 時,
時,![]() ,
,
![]() ,所以
,所以![]() 的解析式為
的解析式為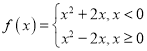 .
.
其圖象如下:
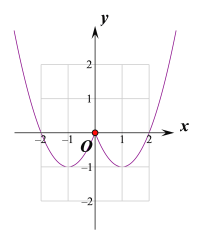
(2)由圖象可知,
當![]() 時,方程
時,方程![]() 無根;
無根;
當![]() 或
或![]() 時,方程
時,方程![]() 有2個根;
有2個根;
當![]() 時,方程
時,方程![]() 有3個根;
有3個根;
當![]() 時,方程
時,方程![]() 有4個根.
有4個根.
(3)由圖象知,點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,點
對稱,點![]() 與點
與點![]() 關于
關于![]() 軸對稱,設點
軸對稱,設點![]() 的坐標是
的坐標是![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標是
的坐標是![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】在一次詩詞知識競賽調查中,發現參賽選手分為兩個年齡(單位:歲)段:![]() ,
,![]() ,其中答對詩詞名句與否的人數如圖所示.
,其中答對詩詞名句與否的人數如圖所示.
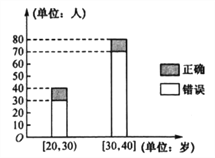
(1)完成下面2×2列聯表;
年齡段 | 正確 | 錯誤 | 合計 |
| |||
| |||
合計 |
(2)是否有90%的把握認為答對詩詞名句與年齡有關,請說明你的理由;
(3)現按年齡段分層抽樣選取6名選手,若從這6名選手中選取3名選手,求3名選手中年齡在![]() 歲范圍人數的分布列和數學期望.
歲范圍人數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合![]() 和常數
和常數![]() ,定義:
,定義:![]() 為集合
為集合![]() 相對
相對![]() 的“余弦方差”.
的“余弦方差”.
(1)若集合![]() ,
,![]() ,求集合
,求集合![]() 相對
相對![]() 的“余弦方差”;
的“余弦方差”;
(2)求證:集合![]() 相對任何常數
相對任何常數![]() 的“余弦方差”是一個與
的“余弦方差”是一個與![]() 無關的定值,并求此定值;
無關的定值,并求此定值;
(3)若集合![]() ,
,![]() ,
,![]() ,相對任何常數
,相對任何常數![]() 的“余弦方差”是一個與
的“余弦方差”是一個與![]() 無關的定值,求出
無關的定值,求出![]() 、
、![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學高考結束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學生進行問卷調查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數據b,c;
(2)判斷是否有99%的把握認為觀看2018年足球世界杯比賽與性別有關;
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發現它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現有問題:在打算觀看2018年足球世界杯比賽的同學中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】基因編輯嬰兒“露露”和“娜娜”出生的消息成了全球矚目的焦點,為了解學生對基因編輯嬰兒的看法,某中學隨機從該校一年級學生中抽取了100人進行調查,抽取的45女生中贊成基因編輯嬰兒的占![]() ,而55名男生中有10人表示贊成基因編輯嬰兒.
,而55名男生中有10人表示贊成基因編輯嬰兒.
(1)完成![]() 列聯表,并回答能否有90%的把握認為“對基因編輯嬰兒是否贊成與性別有關”?
列聯表,并回答能否有90%的把握認為“對基因編輯嬰兒是否贊成與性別有關”?

(2)現從該校不贊成基因編輯嬰兒的學生中,采用分層抽樣的方法抽取7名學生,再從被抽取的7名學生中任取3人,記被抽取的3名學生女生的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com