
【題目】已知數列![]() ,前n項和為
,前n項和為![]() ,對任意的正整數n,都有
,對任意的正整數n,都有![]() 恒成立.
恒成立.
(1)求數列![]() 的通項公式;
的通項公式;
(2)已知關于n的不等式![]() …
…![]() 對一切
對一切![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)已知 ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,試比較
,試比較![]() 與
與![]() 的大小并證明.
的大小并證明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,證明見解析.
,證明見解析.
【解析】
(1)利用數列的遞推關系式化簡,通過累積法轉化求解數列的通項公式.
(2)設![]() ,利用后一項與前一項的差的符號,判斷數列的單調性即可.
,利用后一項與前一項的差的符號,判斷數列的單調性即可.
(3)通過放縮法,利用裂項消項法求解數列的和Tn=c1+c2+c3+…+cn然后推出結果.
(1)由題意,因為2Sn=(n+1)an,
當n≥2時,2Sn-1=nan-1,
兩式相減2an=(n+1)an-nan-1,可得(n-1)an=nan-1(n≥2),
又a1=1≠0,則an≠0,所以![]() ,
,
可得![]() ,
,
累乘得n≥2時,![]() ,
,
n=1時,a1=1也滿足上式,
所以數列![]() 的通項公式為an=n
的通項公式為an=n![]() .
.
(2)設![]() ,
,
則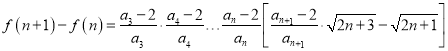
=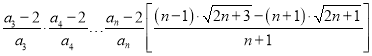
= ,
,
所以f(n)在n≥3,n∈N*上單調遞減,
所以![]() ,即
,即![]() .
.
(3)![]() ,
,
則Tn=c1+c2+c3+…+cn
=![]()
=![]() .
.
所以![]() .
.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】濱海市政府今年加大了招商引資的力度,吸引外資的數量明顯增加.一外商計劃在濱海市投資兩個項目,總投資20億元,其中甲項目的10年收益額![]() (單位:億元)與投資額
(單位:億元)與投資額![]() (單位:億元)滿足
(單位:億元)滿足![]() ,乙項目的10年收益額
,乙項目的10年收益額![]() (單位:億元)與投資額
(單位:億元)與投資額![]() (單位:億元)滿足
(單位:億元)滿足![]() ,并且每個項目至少要投資2億元.設兩個項目的10年收益額之和為
,并且每個項目至少要投資2億元.設兩個項目的10年收益額之和為![]() .
.
(1)求![]() ;
;
(2)如何安排甲、乙兩個項目的投資額,才能使這兩個項目的10年收益額之和![]() 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 截直線
截直線![]() 所得線段的中點坐標為
所得線段的中點坐標為![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 某廠一批產品的次品率為![]() ,則任意抽取其中10件產品一定會發現一件次品
,則任意抽取其中10件產品一定會發現一件次品
B. 擲一枚硬幣,連續出現5次正面向上,第六次出現反面向上的概率與正面向上的概率仍然都為0.5
C. 某醫院治療一種疾病的治愈率為10%,那么前9個病人都沒有治愈,第10個人就一定能治愈
D. 氣象部門預報明天下雨的概率是90%,說明明天該地區90%的地方要下雨,其余10%的地方不會下雨
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 分別為
分別為![]() 關于
關于![]() 軸,原點,
軸,原點,![]() 軸的對稱點,
軸的對稱點,
(1)求四邊形![]() 面積的最大值;
面積的最大值;
(2)當四邊形![]() 最大時,在線段
最大時,在線段![]() 上任取一點
上任取一點![]() ,若過
,若過![]() 的直線與橢圓相交于
的直線與橢圓相交于![]() 兩點,且
兩點,且![]() 中點恰為
中點恰為![]() ,求直線
,求直線![]() 斜率
斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是亞太區域國家與地區加強多邊經濟聯系、交流與合作的重要組織,其宗旨和目標是“相互依存、共同利益,堅持開放性多邊貿易體制和減少區域間貿易壁壘.”2017年
是亞太區域國家與地區加強多邊經濟聯系、交流與合作的重要組織,其宗旨和目標是“相互依存、共同利益,堅持開放性多邊貿易體制和減少區域間貿易壁壘.”2017年![]() 會議于11月10日至11日在越南峴港舉行.某研究機構為了了解各年齡層對
會議于11月10日至11日在越南峴港舉行.某研究機構為了了解各年齡層對![]() 會議的關注程度,隨機選取了100名年齡在
會議的關注程度,隨機選取了100名年齡在![]() 內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分組區間分別為
內的市民進行了調查,并將結果繪制成如圖所示的頻率分布直方圖(分組區間分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
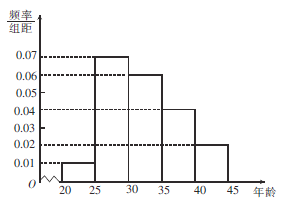
(1)求選取的市民年齡在![]() 內的人數;
內的人數;
(2)若從第3,4組用分層抽樣的方法選取5名市民進行座談,再從中選取2人參與![]() 會議的宣傳活動,求參與宣傳活動的市民中至少有一人的年齡在
會議的宣傳活動,求參與宣傳活動的市民中至少有一人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com