已知f(x),g(x)都是定義在R上的函數，并滿足以下條件：（1）f(x)=2axg(x),(a>0,a
1);（2）g(x)0; (3)f(x) g'(x)< f'(x) g(x)且
,則a=(
)
A.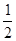
B.2 C. 
D.2或
沖刺100分1號卷系列答案科目：高中數學 來源： 題型：013
已知f(x)、g(x)都是奇函數，f(x)>0的解集是（a2,b）, g(x)>0的解集是
，則f(x)·g(x)>0的解集是（ ）
A．
B．（－b,－a2）
C．
D．
查看答案和解析>>
科目：高中數學 來源：數學教研室 題型：013
，則f(x)·g(x)>0的解集是（ ）
A．
B．（－b,－a2）
C．
D．
查看答案和解析>>
科目：高中數學 來源：2004年高考教材全程總復習試卷·數學 題型：047
已知f(x)為奇函數，g(x)為偶函數，且f(x)＋g(x)＝ax，a＞0且a≠1．
求證：(1)f(2x)＝2f(x)·g(x)．
(2)設f(x)的反函數為f－1(x)，當a＝
－1時，比較f－1[g(x)]與－1的大小關系并證明．
查看答案和解析>>
科目：高中數學 來源：陜西省寶雞市2010屆高三教學質量檢測(二)數學理合試題 題型：013
已知f(x)＝sinx，x∈R，g(x)的圖像與f(x)的圖像交于點(
，0)對稱，則在區間(0，2π)上滿足f(x)≤g(x)的x的范圍是
[
]
[
]
[
]
查看答案和解析>>
科目：高中數學 來源：2011-2012學年河北省高三8月月考理科數學試卷（解析版） 題型：解答題
已知函數f(x)＝ax3＋bx2＋cx在x＝±1處取得極值，且在x＝0處的切線的斜率為－3.
(1)求f(x)的解析式；
(2)若過點A(2，m)可作曲線y＝f(x)的三條切線，求實數m的取值范圍．
【解析】本試題主要考查了導數在研究函數中的運用。第一問，利用函數f(x)＝ax3＋bx2＋cx在x＝±1處取得極值，且在x＝0處的切線的斜率為－3，得到c＝－3 ∴a＝1, f(x)＝x3－3x
(2)中設切點為(x0，x03－3x0)，因為過點A(2，m)，所以∴m－(x03－3x0)＝(3x02－3)(2－x0)分離參數∴m＝－2x03＋6x02－6
然后利用g(x)＝－2x3＋6x2－6函數求導數，判定單調性，從而得到要是有三解，則需要滿足－6<m<2
解：(1)f′(x)＝3ax2＋2bx＋c
依題意
又f′(0)＝－3
∴c＝－3 ∴a＝1 ∴f(x)＝x3－3x
(2)設切點為(x0，x03－3x0)，
∵f′(x)＝3x2－3，∴f′(x0)＝3x02－3
∴切線方程為y－(x03－3x0)＝(3x02－3)(x－x0)
又切線過點A(2，m)
∴m－(x03－3x0)＝(3x02－3)(2－x0)
∴m＝－2x03＋6x02－6
令g(x)＝－2x3＋6x2－6
則g′(x)＝－6x2＋12x＝－6x(x－2)
由g′(x)＝0得x＝0或x＝2
∴g(x)在(－∞，0)單調遞減，(0,2)單調遞增，(2，＋∞)單調遞減．
∴g(x)極小值＝g(0)＝－6，g(x)極大值＝g(2)＝2
畫出草圖知，當－6<m<2時，m＝－2x3＋6x2－6有三解，
所以m的取值范圍是(－6,2)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
