
【題目】(原創,較難)橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,與y軸正半軸交于點B,若
,與y軸正半軸交于點B,若![]() 為等腰直角三角形,且直
為等腰直角三角形,且直![]() 線被圓
線被圓![]() 所截得的弦長為2.
所截得的弦長為2.
(1)求橢圓的方程;(2)直線l與橢圓交于點A、C,線段AC的中點為M,射線MO與橢圓交于點P,點O為![]() 重心,探求
重心,探求![]() 面積
面積![]() 是否為定值,若是求出這個值,若不是求
是否為定值,若是求出這個值,若不是求![]() 的取值范圍
的取值范圍
【答案】(1) ![]() .
.
(2) ![]() 面積
面積![]() 為定值
為定值![]() .
.
【解析】
分析:(1)由![]() 為等腰直角三角形可得
為等腰直角三角形可得![]() ,由直線
,由直線![]() :
:![]() 被圓
被圓![]() 所截得的弦長為2,可得
所截得的弦長為2,可得![]() ,
,![]() ,從而可得橢圓的方程;(2)設直線
,從而可得橢圓的方程;(2)設直線![]() 的方程為
的方程為![]() ,設
,設![]() ,
,![]() ,聯立
,聯立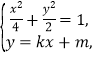 ,利用韋達定理、結合重心坐標公式求出
,利用韋達定理、結合重心坐標公式求出![]() 點坐標,代入橢圓方程可得
點坐標,代入橢圓方程可得![]() ,利用弦長公式、點到直線距離公式以及三角形面積公式可得
,利用弦長公式、點到直線距離公式以及三角形面積公式可得![]() 的面積為
的面積為![]() ,化簡可得結果.
,化簡可得結果.
詳解:(1)由![]() 為等腰直角三角形可得
為等腰直角三角形可得![]() ,直線
,直線![]() :
:![]() 被圓
被圓![]() 所截得的弦長為2,所以
所截得的弦長為2,所以![]() ,
,![]() ,所以橢圓的方程為
,所以橢圓的方程為![]() .
.
(2)若直線![]() 的斜率不存在,則
的斜率不存在,則![]() .
.
若直線![]() 的斜率存在,設直線
的斜率存在,設直線![]() 的方程為
的方程為![]() ,設
,設![]() ,
,![]() ,
,
即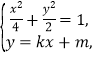 則
則![]() ,
,![]() ,
,![]() ,
,
由題意點![]() 為
為![]() 重心,設
重心,設![]() ,則
,則![]() ,
,![]() ,
,
所以![]() ,
,![]() ,代入橢圓
,代入橢圓![]() ,得
,得
![]() ,整理得
,整理得![]() ,
,
設坐標原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]() 的面積
的面積
![]()
![]()
![]()
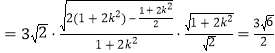 .
.
綜上可得![]() 的面積
的面積![]() 為定值
為定值![]() .
.


科目:高中數學 來源: 題型:
【題目】關于曲線C:![]() ,給出下列五個命題:
,給出下列五個命題:
①曲線C關于直線y=x對稱;
②曲線C關于點![]() 對稱;
對稱;
③曲線C上的點到原點距離的最小值為![]() ;
;
④當![]() 時,曲線C上所有點處的切線斜率為負數;
時,曲線C上所有點處的切線斜率為負數;
⑤曲線C與兩坐標軸所圍成圖形的面積是![]() .
.
上述命題中,為真命題的是_____.(將所有真命題的編號填在橫線上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的導函數為
的導函數為![]() ,且對任意的實數
,且對任意的實數![]() 都有
都有![]() (
(![]() 是自然對數的底數),且
是自然對數的底數),且![]() ,若關于
,若關于![]() 的不等式
的不等式![]() 的解集中恰有兩個整數,則實數
的解集中恰有兩個整數,則實數![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解四川省各景點在大眾中的熟知度,隨機對![]() 歲的人群抽樣了
歲的人群抽樣了![]() 人,回答問題“四川省有哪幾個著名的旅游景點?”統計結果如表.
人,回答問題“四川省有哪幾個著名的旅游景點?”統計結果如表.

組號 | 分組 | 回答正確的人數 | 回答正確的人數 占本組的頻率 |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
第 |
| | |
(1)分別求出![]() 的值;
的值;
(2)從第![]() ,
,![]() ,
,![]() 組回答正確的人中用分層抽樣的方法抽取
組回答正確的人中用分層抽樣的方法抽取![]() 人,求第
人,求第![]() ,
,![]() ,
,![]() 組每組各抽取多少人?
組每組各抽取多少人?
(3)通過直方圖求出年齡的眾數,平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 與圓
與圓![]() 外切于原點
外切于原點![]() ,且兩圓圓心的距離
,且兩圓圓心的距離![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求圓![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)過點![]() 的直線
的直線![]() 與圓
與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,與圓
,與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,且
,且![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,曲邊三角形中,線段![]() 是直線
是直線![]() 的一部分,曲線段
的一部分,曲線段![]() 是拋物線
是拋物線![]() 的一部分.矩形
的一部分.矩形![]() 的頂點分別在線段
的頂點分別在線段![]() ,曲線段
,曲線段![]() 和
和![]() 軸上.設點
軸上.設點![]() ,記矩形
,記矩形![]() 的面積為
的面積為![]() .
.
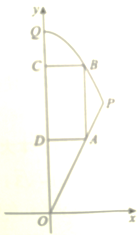
(Ⅰ)求函數![]() 的解析式并指明定義域;
的解析式并指明定義域;
(Ⅱ)求函數![]() 的最大值.
的最大值.
【答案】(Ⅰ) 定義域為![]() ;(Ⅱ) 在
;(Ⅱ) 在![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
【解析】試題分析:( I )根據點![]() 在直線
在直線![]() 上,
上,![]() 在拋物線
在拋物線![]() 上,結合圖形,可得點
上,結合圖形,可得點![]() ,從而可得函數
,從而可得函數![]() 的解析式,聯立直線與拋物線的方程,即可求得定義域;(II)對函數
的解析式,聯立直線與拋物線的方程,即可求得定義域;(II)對函數![]() 求導,利用導數研究函數的單調性,從而可求得函數
求導,利用導數研究函數的單調性,從而可求得函數![]() 的最大值.
的最大值.
試題解析:( I )令![]() ,
,
解得![]()
![]() (舍)
(舍)
因為點![]()
所以![]()
![]() ,
,
其定義域為![]()
(II)因為![]()
令![]() ,得
,得![]() ,
,![]() (舍)
(舍)
所以![]() 的變化情況如下表
的變化情況如下表
|
|
|
|
|
| 0 |
|
|
| 極大 |
|
因為![]() 是函數
是函數![]() 在
在![]() 上的唯一的一個極大值,
上的唯一的一個極大值,
所以在![]() 時,函數
時,函數![]() 取得最大值
取得最大值![]() .
.
點睛:利用導數解答函數最值的一般步驟:第一步:利用![]() 或
或![]() 求單調區間;第二步:解
求單調區間;第二步:解![]() 得兩個根
得兩個根![]() ;第三步:比較兩根同區間端點的大小;第四步:求極值;第五步:比較極值同端點值的大小.
;第三步:比較兩根同區間端點的大小;第四步:求極值;第五步:比較極值同端點值的大小.
【題型】解答題
【結束】
16
【題目】在各項均為正數的數列![]() 中,
中,![]()
![]() 且
且![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 的值;
的值;
(Ⅱ)求證:當![]() 時,
時,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com