
【題目】為迎接2022年冬奧會,北京市組織中學生開展冰雪運動的培訓活動,并在培訓結(jié)束后對學生進行了考核.記X表示學生的考核成績,并規(guī)定X≥85為考核優(yōu)秀.為了了解本次培訓活動的效果,在參加培訓的學生中隨機抽取了30名學生的考核成績,并作成如下莖葉圖.
(1)從參加培訓的學生中隨機選取1人,請根據(jù)圖中數(shù)據(jù),估計這名學生考核優(yōu)秀的概率;
(2)從圖中考核成績滿足X![]() [70,79]的學生中任取3人,設(shè)Y表示這3人重成績滿足
[70,79]的學生中任取3人,設(shè)Y表示這3人重成績滿足![]() ≤10的人數(shù),求Y的分布列和數(shù)學期望.
≤10的人數(shù),求Y的分布列和數(shù)學期望.

【答案】(1)![]() (2)
(2)![]() ,分布列見解析
,分布列見解析
【解析】
(1)根據(jù)莖葉圖得到成績優(yōu)秀的人數(shù),然后根據(jù)古典概型概率公式求解即可.(2)根據(jù)題意先得到![]() 的所有可能取值,然后分別求出對應的概率,進而可得分布列和期望.
的所有可能取值,然后分別求出對應的概率,進而可得分布列和期望.
(1)設(shè)該名學生考核成績優(yōu)秀為事件![]() ,由莖葉圖中的數(shù)據(jù)可以知在30名同學的成績中,優(yōu)秀的為:85,89,90,90,91,92,93,共有7名同學,
,由莖葉圖中的數(shù)據(jù)可以知在30名同學的成績中,優(yōu)秀的為:85,89,90,90,91,92,93,共有7名同學,
所以![]() ,
,
所以可估計這名學生考核優(yōu)秀的概率為![]() .
.
(2)由題意可得![]() 的所有可能取值為
的所有可能取值為![]() ,
,
因為成績![]() 的學生共有8人,其中滿足
的學生共有8人,其中滿足![]() 的學生有
的學生有![]() 人,
人,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以隨機變量![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
所以![]() ,
,
即數(shù)學期望為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】研究機構(gòu)對某校學生往返校時間的統(tǒng)計資料表明:該校學生居住地到學校的距離![]() (單位:千米)和學生花費在上學路上的時間
(單位:千米)和學生花費在上學路上的時間![]() (單位:分鐘)有如下的統(tǒng)計資料:
(單位:分鐘)有如下的統(tǒng)計資料:
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統(tǒng)計資料表明![]() 與
與![]() 有線性相關(guān)關(guān)系,試求:
有線性相關(guān)關(guān)系,試求:
(1)判斷![]() 與
與![]() 是否有很強的線性相關(guān)性?
是否有很強的線性相關(guān)性?
(相關(guān)系數(shù)![]() 的絕對值大于0.75時,認為兩個變量有很強的線性相關(guān)性,精確到0.01)
的絕對值大于0.75時,認為兩個變量有很強的線性相關(guān)性,精確到0.01)
(2)求線性回歸方程![]() (精確到0.01);
(精確到0.01);
(3)將![]() 分鐘的時間數(shù)據(jù)
分鐘的時間數(shù)據(jù)![]() 稱為美麗數(shù)據(jù),現(xiàn)從這6個時間數(shù)據(jù)
稱為美麗數(shù)據(jù),現(xiàn)從這6個時間數(shù)據(jù)![]() 中任取2個,求抽取的2個數(shù)據(jù)全部為美麗數(shù)據(jù)的概率.
中任取2個,求抽取的2個數(shù)據(jù)全部為美麗數(shù)據(jù)的概率.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
參考公式: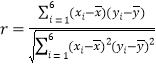 ,
,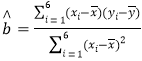
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知變量![]() 、
、![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() ,且變量
,且變量![]() 、
、![]() 之間的一-組相關(guān)數(shù)據(jù)如下表所示,則下列說法錯誤的是( )
之間的一-組相關(guān)數(shù)據(jù)如下表所示,則下列說法錯誤的是( )
|
|
|
|
|
|
|
|
|
|
A.可以預測,當![]() 時,
時,![]() B.
B.![]()
C.變量![]()
![]() 之間呈負相關(guān)關(guān)系D.該回歸直線必過點
之間呈負相關(guān)關(guān)系D.該回歸直線必過點![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,某人工景觀湖外圍有兩條相互垂直的直線型公路ll,l2,且ll和l2交于點O.為了方便游客游覽,計劃修建一條連接公路與景觀湖的直線型公路AB.景觀湖的輪廓可以近似看成一個圓心為O,半徑為2百米的圓,且公路AB與圓O相切,圓心O到ll,l2的距離均為5百米,設(shè)OAB=![]() ,AB長為L百米.
,AB長為L百米.
(1)求L關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)當![]() 為何值時,公路AB的長度最短?
為何值時,公路AB的長度最短?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() 分別在
分別在![]() 、
、![]() 處取得極小值、極大值.
處取得極小值、極大值.![]() 平面上點
平面上點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,該平面上動點
,該平面上動點![]() 滿足
滿足![]() ,點
,點![]() 是點
是點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點.
的對稱點.
(Ⅰ)求點![]() 、
、![]() 的坐標;
的坐標;
(Ⅱ)求動點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)是定義在![]() 上的單調(diào)函數(shù),且對任意的x∈
上的單調(diào)函數(shù),且對任意的x∈![]() 都有
都有![]() ,則方程
,則方程![]() 的一個根所在的區(qū)間是( )
的一個根所在的區(qū)間是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題p:x2+mx+1=0有兩個不等的負根;命題q:4x2+4(m﹣2)x+1=0無實根.若命題p與命題q有且只有一個為真,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,![]() 為橢圓
為橢圓![]() 的左頂點,過
的左頂點,過![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 是
是![]() 的中點.
的中點.
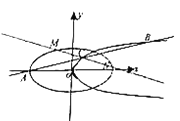
(1)求證:點![]() 的橫坐標是定值,并求出該定值;
的橫坐標是定值,并求出該定值;
(2)若直線![]() 過
過![]() 點,且傾斜角和直線
點,且傾斜角和直線![]() 的傾斜角互補,交橢圓于
的傾斜角互補,交橢圓于![]() 、
、![]() 兩點,求
兩點,求![]() 的值,使得
的值,使得![]() 的面積最大.
的面積最大.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com