【題目】已知
，
（
，
），
且
的圖象上相鄰兩條對稱軸之間的距離為
．
（1）求函數的單調遞增區間；
（2）若
的內角
，
，
的對邊分別為
，
，
，且
，
，
，求，的值及
邊上的中線．
【答案】（1）
．（2）
，
，
．
【解析】
（1）由平面向量數量積的坐標運算，結合降冪公式及輔助角公式化簡三角函數式，根據鄰兩條對稱軸之間的距離求得
，即可得函數
解析式，結合正弦函數的圖象與性質即可求得的單調遞增區間；
（2）由
代入解析式可得
的值；由正弦定理與余弦定理，代入已知條件可得
的值；設AC邊上的中線為BD，由
，結合平面向量數量積定義即可求得
，即為
邊上的中線長.
（1）由平面向量數量積的坐標運算，結合降冪公式及輔助角公式化簡可得
由的圖象上相鄰兩條對稱軸之間的距離為
得，
，
所以
．
令
得，
所以的單調遞增區間為．
（2）
解得
，
由
得
，
由余弦定理可知
，代入可得
解得，
記AC邊上的中線為BD，
．
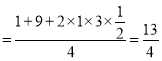所以
，即邊上的中線為.
科目：高中數學 來源： 題型：
【題目】已知菱形ABCD中，∠BAD=60°，AC與BD相交于點O．將△ABD沿BD折起，使頂點A至點M，在折起的過程中，下列結論正確的是（ ）
A.BD⊥CM
B.存在一個位置，使△CDM為等邊三角形
C.DM與BC不可能垂直
D.直線DM與平面BCD所成的角的最大值為60°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A，B關于坐標原點O對稱，
，以M為圓心的圓過A，B兩點，且與直線
相切，若存在定點P，使得當A運動時，
為定值，則點P的坐標為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2019年春節假期，旅游過年持續火爆.特別是：東北雪鄉、夢回大唐、江南水鄉、三亞之行這四條路線受到廣大人民的熱播.現有2個家庭準備去這四個地方旅游，假設每個家庭均從這四條路線中任意選取一條路線去旅源，則兩個家庭選擇同一路線的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線E：
過點
，過拋物線E上一點
作兩直線PM，PN與圓C：
相切，且分別交拋物線E于M、N兩點．
（1）求拋物線E的方程，并求其焦點坐標和準線方程；
（2）若直線MN的斜率為
，求點P的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
的坐標分別為
，
.三角形
的兩條邊
，
所在直線的斜率之積是
.
（1）求點
的軌跡方程；
（2）設直線方程為
，直線
方程為
，直線交于
，點，
關于
軸對稱，直線
與軸相交于點
.若
的面積為
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我市某區2018年房地產價格因“棚戶區改造”實行貨幣化補償，使房價快速走高，為抑制房價過快上漲，政府從2019年2月開始采用實物補償方式（以房換房），3月份開始房價得到很好的抑制，房價漸漸回落，以下是2019年2月后該區新建住宅銷售均價的數據：
月份 | 3 | 4 | 5 | 6 | 7 |
價格 | 83 | 82 | 80 | 78 | 77 |
（1）研究發現，3月至7月的各月均價
（百元/平方米）與月份
之間具有較強的線性相關關系，求價格（百元/平方米）關于月份的線性回歸方程；
（2）用
表示用（1）中所求的線性回歸方程得到的與
對應的銷售均價的估計值，3月份至7月份銷售均價估計值與實際相應月份銷售均價
差的絕對值記為
，即
，
.若
，則將銷售均價的數據稱為一個“好數據”，現從5個銷售均價數據中任取
參考公式：回歸方程系數公式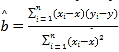
，
；參考數據：
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了貫徹落實黨中央精準扶貧決策，某市將其低收入家庭的基本情況經過統計繪制如圖，其中各項統計不重復．若該市老年低收入家庭共有900戶，則下列說法錯誤的是（ ）
A.該市總有 15000 戶低收入家庭
B.在該市從業人員中，低收入家庭共有1800戶
C.在該市無業人員中，低收入家庭有4350戶
D.在該市大于18歲在讀學生中，低收入家庭有 800 戶
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在等腰梯形
中，兩腰
，底邊
是
的三等分點，
是
的中點.分別沿
將四邊形
和
折起，使
重合于點
，得到如圖2所示的幾何體.在圖2中，
分別為
的中點.
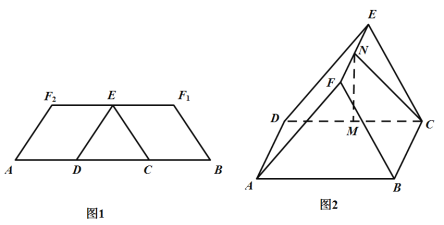
(1)證明:
平面
(2)求幾何體
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com