
��֪�E�A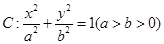 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��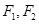 ���c(di��n)
���c(di��n)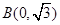 ����S��һ��(g��)���c(di��n)��
����S��һ��(g��)���c(di��n)��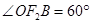 .
.
��1����E�A �ķ��̣�
�ķ��̣�
��2����D���^(gu��)�ҽ��c(di��n)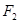 ����б�ʞ�
����б�ʞ�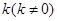 ��ֱ��
��ֱ��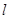 �c�E�A
�c�E�A �ཻ��
�ཻ��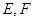 ���c(di��n)��
���c(di��n)�� ��E�A������c(di��n)��ֱ��
��E�A������c(di��n)��ֱ��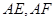 �քe��ֱ��
�քe��ֱ��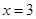 ���c(di��n)
���c(di��n)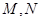 ������
������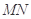 �����c(di��n)��
�����c(di��n)��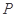 ��ӛֱ��
��ӛֱ��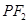 ��б�ʞ�
��б�ʞ� .
.
���C:  �鶨ֵ.
�鶨ֵ.
��1��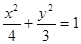 ����2��ԔҊ(ji��n)����
����2��ԔҊ(ji��n)����
����ԇ�}��������1�����c(di��n)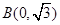 ����S��һ��(g��)���c(di��n)��֪
����S��һ��(g��)���c(di��n)��֪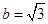 ����ֱ��������
����ֱ��������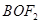 ����֪
����֪ ���Ķ��ɵ�
���Ķ��ɵ�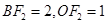 ����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/54/c/lxutv.png" style="vertical-align:middle;" />������
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/54/c/lxutv.png" style="vertical-align:middle;" />������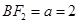 .��2���O(sh��)�^(gu��)�c(di��n)
.��2���O(sh��)�^(gu��)�c(di��n)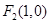 ��ֱ��
��ֱ��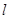 ���̞飺
���̞飺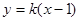 ���c�E�A����(li��n)����ȥ
���c�E�A����(li��n)����ȥ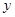 ������P(gu��n)��
������P(gu��n)��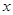 ��һԪ���η��̣��O(sh��)�c(di��n)
��һԪ���η��̣��O(sh��)�c(di��n) ��
��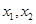 �鷽�̵ăɸ����ɵø��cϵ��(sh��)���P(gu��n)ϵ����б�ʹ�ʽ�ɷքe���ֱ��
�鷽�̵ăɸ����ɵø��cϵ��(sh��)���P(gu��n)ϵ����б�ʹ�ʽ�ɷքe���ֱ��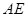 ��ֱ��
��ֱ��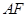 ��б�ʣ�����(j��)�c(di��n)бʽ�ɵÃ�ֱ�����̡�ֱ��
��б�ʣ�����(j��)�c(di��n)бʽ�ɵÃ�ֱ�����̡�ֱ��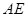 ��ֱ��
��ֱ��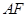 �քe�cֱ��
�քe�cֱ��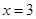 (li��n)�������c(di��n)
(li��n)�������c(di��n) ������(j��)���c(di��n)����(bi��o)��ʽ�ɵ��c(di��n)
������(j��)���c(di��n)����(bi��o)��ʽ�ɵ��c(di��n) ����(bi��o)������(j��)б�ʹ�ʽ��
����(bi��o)������(j��)б�ʹ�ʽ�� �������C��
�������C�� �鶨ֵ��
�鶨ֵ��
�⣺��1���ɗl����֪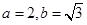 �� 2��
�� 2��
������E�A���̞�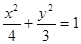 . 4��
. 4��
��2���O(sh��)�^(gu��)�c(di��n)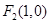 ��ֱ��
��ֱ��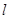 ���̞飺
���̞飺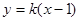 . 5��
. 5��
��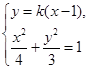 �ɵã�
�ɵã�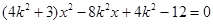 6��
6��
��?y��n)��c(di��n)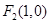 �ڙE�A��(n��i)������ֱ��
�ڙE�A��(n��i)������ֱ�� �͙E�A���ཻ����
�͙E�A���ཻ����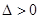 �����.
�����.
�O(sh��)�c(di��n) ���t
���t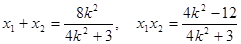 . 8��
. 8��
��?y��n)�ֱ��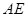 �ķ��̞飺
�ķ��̞飺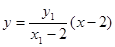 ��
��
ֱ��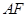 �ķ��̞飺
�ķ��̞飺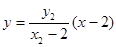 �� 9��
�� 9��
��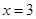 ���ɵ�
���ɵ�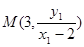 ��
�� ��
��
�����c(di��n) ������(bi��o)
������(bi��o)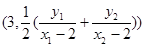 . 10��
. 10��
ֱ��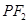 ��б�ʞ�
��б�ʞ�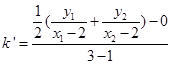
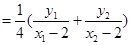
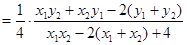
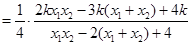 12��
12��
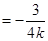
����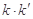 �鶨ֵ
�鶨ֵ . 13��
. 13��
���c(di��n)��1�E�A�ĺ�(ji��n)�����|(zh��)�����̣�2ֱ���c�E�A��λ���P(gu��n)ϵ��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D, ������(bi��o)ԭ�c(di��n),�E�A
������(bi��o)ԭ�c(di��n),�E�A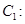
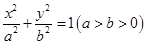 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��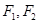 ,�x���ʞ�
,�x���ʞ�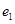 ;�p����
;�p����
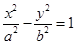 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��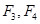 ,�x���ʞ�
,�x���ʞ�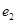 ,��֪
,��֪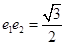 ,��
,��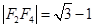 .
.
(1)��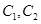 �ķ���;
�ķ���;
(2)�^(gu��) �c(di��n)��
�c(di��n)��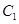 �IJ���ֱ��
�IJ���ֱ�� �S����
�S����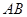 ,
,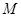 ��
��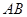 �����c(di��n),��(d��ng)ֱ��
�����c(di��n),��(d��ng)ֱ��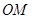 �c
�c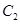 ����
����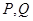 ���c(di��n)�r(sh��),����߅��
���c(di��n)�r(sh��),����߅�� ��e����Сֵ.
��e����Сֵ.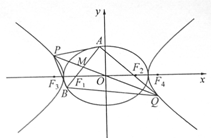
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��12�֣���2011•��������D��ֱ��l��y=x+b�c���タC��x2=4y�������c(di��n)A��
������(sh��)��(sh��)b��ֵ��
���������c(di��n)A��A�ģ����c���タC�Ĝ�(zh��n)�����еĈA�ķ��̣�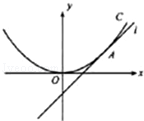
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�c(di��n) �ǙE�A
�ǙE�A ����һ�c(di��n)���c(di��n)
����һ�c(di��n)���c(di��n)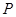 ��ֱ��
��ֱ��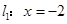 �ľ��x��
�ľ��x��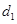 �����c(di��n)
�����c(di��n)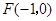 �ľ��x��
�ľ��x��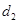 ����
����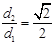 ��ֱ��
��ֱ��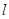 �c�E�A
�c�E�A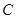 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)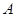 ��
��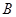 (
(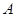 ��
��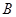 ����
����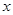 �S�Ϸ�)����
�S�Ϸ�)����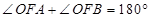 ��
��
��1����E�A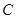 �ķ��̣�
�ķ��̣�
��2����(d��ng)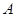 ��E�A�c
��E�A�c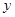 �S�����S�Ľ��c(di��n)�r(sh��)����ֱ��
�S�����S�Ľ��c(di��n)�r(sh��)����ֱ��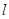 ���̣�
���̣�
��3����(du��)�ڄ�(d��ng)ֱ��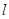 ���Ƿ����һ��(g��)���c(di��n)���o(w��)Փ
���Ƿ����һ��(g��)���c(di��n)���o(w��)Փ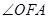 ���׃����ֱ��
���׃����ֱ��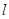 ����(j��ng)�^(gu��)�˶��c(di��n)�������ڣ����ԓ���c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
����(j��ng)�^(gu��)�˶��c(di��n)�������ڣ����ԓ���c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ�ķ��̞�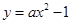 ��ֱ��
��ֱ��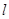 �ķ��̞�
�ķ��̞�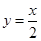 ���c(di��n)
���c(di��n)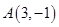 �P(gu��n)��ֱ��
�P(gu��n)��ֱ��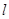 �Č�(du��)�Q�c(di��n)�ڒ��タ�ϣ�
�Č�(du��)�Q�c(di��n)�ڒ��タ�ϣ�
��1�����タ�ķ��̣�
��2����֪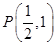 ���c(di��n)
���c(di��n) �ǒ��タ�Ľ��c(di��n)��
�ǒ��タ�Ľ��c(di��n)�� �ǒ��タ�ϵĄ�(d��ng)�c(di��n)����
�ǒ��タ�ϵĄ�(d��ng)�c(di��n)����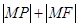 ����Сֵ���˕r(sh��)�c(di��n)
����Сֵ���˕r(sh��)�c(di��n) ������(bi��o)��
������(bi��o)��
��3���O(sh��)�c(di��n) ��
�� �ǒ��タ�ϵĄ�(d��ng)�c(di��n)���c(di��n)
�ǒ��タ�ϵĄ�(d��ng)�c(di��n)���c(di��n) �ǒ��タ�c
�ǒ��タ�c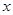 �S�����S���c(di��n)��
�S�����S���c(di��n)�� ����
���� ��ֱ����c(di��n)��ֱ�������Σ�ԇ̽��ֱ��
��ֱ����c(di��n)��ֱ�������Σ�ԇ̽��ֱ�� �Ƿ�(j��ng)�^(gu��)���c(di��n)������(j��ng)�^(gu��)��������c(di��n)������(bi��o)��������(j��ng)�^(gu��)��Ո(q��ng)�f(shu��)�����ɣ�
�Ƿ�(j��ng)�^(gu��)���c(di��n)������(j��ng)�^(gu��)��������c(di��n)������(bi��o)��������(j��ng)�^(gu��)��Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����С�}�M��12�֣�
��ֱ֪�� ��
��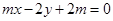
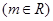 �͙E�A
�͙E�A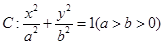 ���E�AC���x���ʞ�
���E�AC���x���ʞ�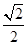 ���B�Y(ji��)�E�A���Ă�(g��)��c(di��n)�γ���߅�ε���e��
���B�Y(ji��)�E�A���Ă�(g��)��c(di��n)�γ���߅�ε���e�� .
.
��1����E�AC�ķ��̣�
��2����ֱ�� �c�E�AC�Ѓɂ�(g��)��ͬ�Ľ��c(di��n)����(sh��)��(sh��)m��ȡֵ������
�c�E�AC�Ѓɂ�(g��)��ͬ�Ľ��c(di��n)����(sh��)��(sh��)m��ȡֵ������
��3����(d��ng)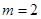 �r(sh��)���O(sh��)ֱ��
�r(sh��)���O(sh��)ֱ�� �cy�S�Ľ��c(di��n)��P��M��E�AC�ϵĄ�(d��ng)�c(di��n)����PM�L(zh��ng)�ȵ����ֵ.
�cy�S�Ľ��c(di��n)��P��M��E�AC�ϵĄ�(d��ng)�c(di��n)����PM�L(zh��ng)�ȵ����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪?ji��ng)ӈA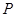 �c�A
�c�A �������c�A
���У����c�A ����(n��i)�У�ӛ�A��
����(n��i)�У�ӛ�A��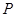 ��܉�E������
��܉�E������ ���O(sh��)
���O(sh��) ������
������ �ϵ�һ��(g��)����
�ϵ�һ��(g��)���� �S�ϵĄ�(d��ng)�c(di��n)��
�S�ϵĄ�(d��ng)�c(di��n)�� ������(bi��o)ԭ�c(di��n)���^(gu��)�c(di��n)
������(bi��o)ԭ�c(di��n)���^(gu��)�c(di��n) ��
�� ��ƽ�о�������
��ƽ�о������� ��
�� �ɂ�(g��)��ͬ���c(di��n).
�ɂ�(g��)��ͬ���c(di��n).
��1�������� �ķ��̣�
�ķ��̣�
��2��ԇ̽�� ��
�� �ı�ֵ�ܷ��һ��(g��)����(sh��)�����ܣ�����@��(g��)����(sh��)�������ܣ�Ո(q��ng)�f(shu��)�����ɣ�
�ı�ֵ�ܷ��һ��(g��)����(sh��)�����ܣ�����@��(g��)����(sh��)�������ܣ�Ո(q��ng)�f(shu��)�����ɣ�
��3��ӛ ����e��
����e�� ��
�� ����e��
����e�� ����
���� ����
���� �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��2011•�㽭����֪���タC1��x2=y���AC2��x2+��y��4��2=1�ĈA�Ğ��c(di��n)M
��1�����c(di��n)M�����タC1�Ĝ�(zh��n)���ľ��x��
��2����֪�c(di��n)P�ǒ��タC1��һ�c(di��n)������ԭ�c(di��n)�����^(gu��)�c(di��n)P���AC2�ăɗl�о��������タC1��A��B���c(di��n)�����^(gu��)M��P���c(di��n)��ֱ��l��ֱ��AB����ֱ��l�ķ��̣�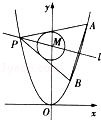
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���O(sh��)���LjA �ϵĄ�(d��ng)�c(di��n)���c(di��n)���ǣ���
�ϵĄ�(d��ng)�c(di��n)���c(di��n)���ǣ��� �S��ͶӰ���͞�PD��һ�c(di��n)����
�S��ͶӰ���͞�PD��һ�c(di��n)����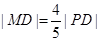 ��
��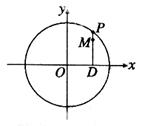
��1����(d��ng)P�ڈA���\(y��n)��(d��ng)�r(sh��)�����c(di��n)M��܉�EC�ķ��̣�
��2�����^(gu��)�c(di��n)��3��0����б�ʞ�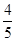 ��ֱ����C���ؾ��ε��L(zh��ng)�ȣ�
��ֱ����C���ؾ��ε��L(zh��ng)�ȣ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com