Question

在△ABC中，已知.

(1)判斷△ABC的形狀，并說明理由;

(2)建立適當的直角坐標系，求△ABC的內切圓的方程;

(3)求PA²+PB²+PC²的最大值和最小值，并求出取到最大值和最小值時點P的坐標;

(4)若Q是△ABC的外接圓上的一個動點，則Q點在何處，QA²+QB²+QC²有最大值或最小值?試求出最值.

Answer 1

解析：先利用正弦定理或余弦定理判斷△ABC的形狀后，建立適當坐標系，關鍵是抓住△ABC的特征來建系，求出內切圓的方程，其次點P在內切圓上，P點的設法有兩種，一是普通設法,P(x,y),|PA|²+|PB|²+|PC|²都用x、y表示，進行化簡，最后化成關于x、y的一次式，注意到x、y的取值范圍，即可以求出最大值和最小值；二是利用圓的參數方程來設，P(x₀+rcosθ,y₀+rsinθ),PA²+PB²+PC²寫成θ的函數式，然后利用三角函數性質求解.第（4）題也是同樣的策略.

(1)解法一:

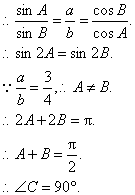
∴△ABC是直角三角形.?

解法二: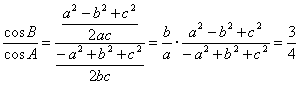

∴a²-b²+c²=(-a²+b²+c²).?

∴a²+b²=c².?

∴△ABC是直角三角形.

(2)解:建立直角坐標系，

令C(0,0),A(8,0),B(0,6),

∴圓心(2,2).

∴內切圓(x-2)²+(y-2)²=2²=4.

(3)解法一:設P點(x,y)(0≤x≤4,0≤y≤4).?

PA²+PB²+PC²=(x-8)²+y²+(x-0)²+(y-6)²+x²+y²

=3x²+3y²-16x-12y+100?

=3(4x+4y-4)-16x-12y+100

=-4x+88.?

∵0≤x≤4,?

∴(PA²+PB²+PC²)_max=88,?

∴P(0,2);?

(PA²+PB²+PC²)_max=-4×4+88=72,?

∴P(4,2).?

解法二:∵點P在內切圓上,?

∴設P(2+2cosθ,2+2sinθ).?

∴PA²+PB²+PC²=(2+2cosθ-8)²+(2+2sinθ)²+(2+2cosθ)²+(2+2sinθ-6)²+(2+2cosθ)²+(2+2sinθ)²=80-8cosθ.?

∴當cosθ=1時，(PA²+PB²+PC²)_min=72.?

∴P(4,2).?

當cosθ=-1時，(PA²+PB²+PC²)_max=88,?

∴P(0,2).

(4)解:∵A、B、C均在外接圓上,

∴設圓方程為x²+y²+Dx+Ey+F=0.?

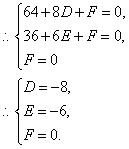
∴x²+y²-8x-6y=0,

∴(x-4)²+(y-3)²=25.?

設Q(x,y),

QA²+QB²+QC²=(x-8)²+y²+x²+(y-6)²+x²+y²=3x²+3y²-16x-12y+100=3×(8x+6y)-16x-12y+100=8x+6y+100,?

令x=5cosθ+4,y=5sinθ+3,?

∴QA²+QB²+QC²=40cosθ+30sinθ+150=50cos(θ-φ)+150(tanφ=),

∴(QA²+QB²+QC²)_max=200,Q(8,6),

(QA²+QB²+QC²)_min=100,Q(0,0).