
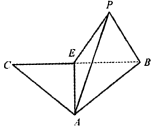
 等腰三角形ABC,E為底邊BC的中點,沿AE折疊,如圖,將C折到點P的位置,使P-AE-C為120°,設點P在面ABE上的射影為H.
等腰三角形ABC,E為底邊BC的中點,沿AE折疊,如圖,將C折到點P的位置,使P-AE-C為120°,設點P在面ABE上的射影為H.分析 (1)推導出AE⊥面EPB,∠CEP為二面角C-AE-P的平面角,從而EH=$\frac{1}{2}$EP=$\frac{1}{2}$EB,由此能證明H為EB的中點.
(2)過H作HM⊥AB于M,連PM,過H作HN⊥PM于N,連BN,則HN為H到平面ABP的距離,由此能求出結果.
解答  證明:(1)依題意,AE⊥BC,則AE⊥EB,AE⊥EP,EB∩EP=E.
證明:(1)依題意,AE⊥BC,則AE⊥EB,AE⊥EP,EB∩EP=E.
∴AE⊥面EPB.
故∠CEP為二面角C-AE-P的平面角,則點P在面ABE上的射影H在EB上.
由∠CEP=120°,得∠PEB=60°.…(3分)
∴EH=$\frac{1}{2}$EP=$\frac{1}{2}$EB.
∴H為EB的中點.…(6分)
解:(2)過H作HM⊥AB于M,連PM,過H作HN⊥PM于N,連BN,
則有三垂線定理得AB⊥面PHM.
即面PHM⊥面PAB,
∴HN⊥面PAB.∴HN為H到平面ABP的距離.…(9分)
依題意,BE=$\frac{1}{2}BC=2$.BH=$\frac{1}{2}BE=1$.
在△HMB中,HM=$\frac{\sqrt{2}}{2}$,
在△EPB中,PH=$\sqrt{3}$,
∴在Rt△PHM中,HN=$\frac{\sqrt{21}}{7}$.…(12分)
點評 本題考查點為線段中點的證明,考查點到平面的距離的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com