
【題目】已知函數f(x)=x2﹣2ax﹣3
(1)若函數在f(x)的單調遞減區間(﹣∞,2],求函數f(x)在區間[3,5]上的最大值.
(2)若函數在f(x)在單區間(﹣∞,2]上是單調遞減,求函數f(1)的最大值.
【答案】
(1)解:由函數f(x)的單調遞減區間(﹣∞,2],
∴a=2;
∴f(x)=(x﹣2)2﹣7,
∴函數f(x)在區間[3,5]上單調遞增,
∴f(x)的最大值在x=5處取到,f(5)=32﹣7=2
(2)解:由函數在f(x)在區間(﹣∞,2]上是單調遞減,得a≥2,
∴f(1)=﹣2﹣2a≤﹣6.
∴函數f(1)的最大值為﹣6
【解析】(1)由函數f(x)的單調遞減區間(﹣∞,2],可得a=2,可得函數f(x)在區間[3,5]上單調遞增,即可得出.(2)由函數在f(x)在區間(﹣∞,2]上是單調遞減,得a≥2,即可得出.
【考點精析】根據題目的已知條件,利用二次函數的性質的相關知識可以得到問題的答案,需要掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.


科目:高中數學 來源: 題型:
【題目】某校高三年級在高校自主招生期間,把學生的平時成績按“百分制”折算并排序,選出前300名學生,并對這300名學生按成績分組,第一組[75,80),第二組[80,85),第三組[85,90),第四組[90,95),第五組[95,100],如圖為頻率分布直方圖的一部分,其中第五組、第一組、第四組、第二組、第三組的人數依次成等差數列. (Ⅰ)請在圖中補全頻率分布直方圖;
(Ⅱ)若B大學決定在成績高的第4,5組中用
分層抽樣的方法抽取6名學生,并且分成2組,每組3人
進行面試,求95分(包括95分)以上的同學被分在同一個小組的概率.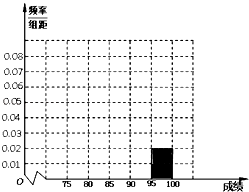
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2﹣2x﹣2ay+a2﹣24=0(a∈R)的圓心在直線2x﹣y=0上.
(1)求實數a的值;
(2)求圓C與直線l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)相交弦長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)= ![]() 滿足f(0)=0.
滿足f(0)=0.
(1)求a,f(﹣2)的值,判斷函數f(x)的奇偶性并說明理由;
(2)判斷該函數在R上的單調性(不要求證明),解不等式f(x2+x)< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,定義在[﹣1,5]上的函數f(x)由一段線段和拋物線的一部分組成. (Ⅰ)求函數f(x)的解析式;
(Ⅱ)指出函數f(x)的自變量x在什么范圍內取值時,函數值大于0,小于0或等于0(不需說理由).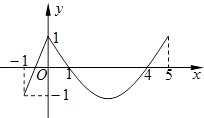
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱柱ABC﹣A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是邊長為2的等邊三角形,AA′=3,E、F分別在棱AA′,CC′上,且AE=C′F=2. 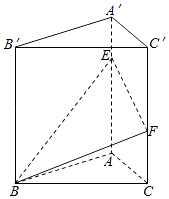
(1)求證:BB′⊥底面ABC;
(2)在棱A′B′上是否存在一點M,使得C′M∥平面BEF,若存在,求 ![]() 值,若不存在,說明理由;
值,若不存在,說明理由;
(3)求棱錐A′﹣BEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosλθ,cos(10﹣λ)θ),
=(cosλθ,cos(10﹣λ)θ), ![]() =(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
=(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]() ⊥
⊥ ![]() ,求θ;
,求θ;
(3)若θ= ![]() ,求證:
,求證: ![]() ∥
∥ ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com