
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為菱形,∠DAB=60°,PD⊥底面ABCD,PD=DC=2,E,F,G分別是AB,PB,CD的中點(diǎn).
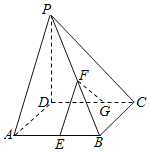
(1)求證:AC⊥PB;
(2)求證:GF∥平面PAD;
(3)求點(diǎn)G到平面PAB的距離.
【答案】(1)證明見(jiàn)解析 (2)證明見(jiàn)解析 (3)![]()
【解析】
(1)由題知,證明AC⊥平面![]() 即可.
即可.
(2) 取PA中點(diǎn)H,連接FH,HD,再證明![]() 即可.
即可.
(3)利用轉(zhuǎn)換法與等體積法VG﹣PAB=VD﹣PAB=VP﹣ABD計(jì)算即可.
(1)證明:如圖,連接AC,BD,
因?yàn)?/span>PD⊥面ABCD,且AC平面ABCD,
所以AC⊥PD,
又因?yàn)樗倪呅?/span>ABCD為菱形,
所以AC⊥BD,
又PD∩BD=D,PD,BD平面PBD,
所以AC⊥平面PBD,
又PB平面PBD,
所以AC⊥PB;
(2)證明:如圖取PA中點(diǎn)H,連接FH,HD,
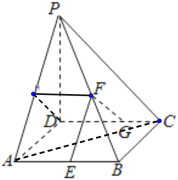
因?yàn)?/span>F為PB中點(diǎn),
所以HF∥AB,且HF![]() AB,
AB,
又因?yàn)樗倪呅?/span>ABCD為菱形,且G為CD中點(diǎn),
所以DG∥AB,且DG![]() AB,
AB,
所以HF∥DG,且HF=DG,
所以四邊形HDGF為平行四邊形,
所以GF∥HD,
因?yàn)?/span>GF平面PAD,HD平面PAD,
所以GF∥平面PAD,
(3)解:設(shè)G到平面PAB的距離為h,
因?yàn)?/span>DC∥AB,DC平面PAB,AB平面PAB,
所以DC∥平面PAB,
所以VG﹣PAB=VD﹣PAB=VP﹣ABD,
所以![]() ,
,
所以h![]() ,
,
所以G到平面PAB的距離為![]() .
.


 時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案
時(shí)刻準(zhǔn)備著暑假作業(yè)原子能出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某電子商務(wù)平臺(tái)的管理員隨機(jī)抽取了1000位上網(wǎng)購(gòu)物者,并對(duì)其年齡(在10歲到69歲之間)進(jìn)行了調(diào)查,統(tǒng)計(jì)情況如下表所示.
年齡 |
|
|
|
|
|
|
人數(shù) | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三個(gè)年齡段的上網(wǎng)購(gòu)物的人數(shù)依次構(gòu)成遞減的等比數(shù)列.
三個(gè)年齡段的上網(wǎng)購(gòu)物的人數(shù)依次構(gòu)成遞減的等比數(shù)列.
(1)求![]() 的值;
的值;
(2)若將年齡在![]() 內(nèi)的上網(wǎng)購(gòu)物者定義為“消費(fèi)主力軍”,其他年齡段內(nèi)的上網(wǎng)購(gòu)物者定義為“消費(fèi)潛力軍”.現(xiàn)采用分層抽樣的方式從參與調(diào)查的1000位上網(wǎng)購(gòu)物者中抽取5人,再?gòu)倪@5人中抽取2人,求這2人中至少有一人是消費(fèi)潛力軍的概率.
內(nèi)的上網(wǎng)購(gòu)物者定義為“消費(fèi)主力軍”,其他年齡段內(nèi)的上網(wǎng)購(gòu)物者定義為“消費(fèi)潛力軍”.現(xiàn)采用分層抽樣的方式從參與調(diào)查的1000位上網(wǎng)購(gòu)物者中抽取5人,再?gòu)倪@5人中抽取2人,求這2人中至少有一人是消費(fèi)潛力軍的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2017高考新課標(biāo)Ⅲ,理19)如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
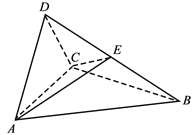
(1)證明:平面ACD⊥平面ABC;
(2)過(guò)AC的平面交BD于點(diǎn)E,若平面AEC把四面體ABCD分成體積相等的兩部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】以橢圓![]() 的離心率為
的離心率為![]() ,以其四個(gè)頂點(diǎn)為頂點(diǎn)的四邊形的面積等于
,以其四個(gè)頂點(diǎn)為頂點(diǎn)的四邊形的面積等于![]() .
.
![]() 1
1![]() 求橢圓
求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
![]() 2
2![]() 過(guò)原點(diǎn)且斜率不為0的直線
過(guò)原點(diǎn)且斜率不為0的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),
兩點(diǎn),![]() 是橢圓
是橢圓![]() 的右頂點(diǎn),直線
的右頂點(diǎn),直線![]() 分別與
分別與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,問(wèn):以
,問(wèn):以![]() 為直徑的圓是否恒過(guò)
為直徑的圓是否恒過(guò)![]() 軸上的定點(diǎn)?若恒過(guò)
軸上的定點(diǎn)?若恒過(guò)![]() 軸上的定點(diǎn),請(qǐng)求出該定點(diǎn)的坐標(biāo);若不恒過(guò)
軸上的定點(diǎn),請(qǐng)求出該定點(diǎn)的坐標(biāo);若不恒過(guò)![]() 軸上的定點(diǎn),請(qǐng)說(shuō)明理由.
軸上的定點(diǎn),請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在四棱錐![]() 中,底面ABCD是邊長(zhǎng)為6的菱形,且
中,底面ABCD是邊長(zhǎng)為6的菱形,且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,F是棱PA上的一個(gè)動(dòng)點(diǎn),E為PD的中點(diǎn).
,F是棱PA上的一個(gè)動(dòng)點(diǎn),E為PD的中點(diǎn).
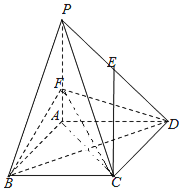
![]() Ⅰ
Ⅰ![]() 求證:
求證:![]() .
.
![]() Ⅱ
Ⅱ![]() 若
若![]() .
.
![]() 求PC與平面BDF所成角的正弦值;
求PC與平面BDF所成角的正弦值;
![]() 側(cè)面PAD內(nèi)是否存在過(guò)點(diǎn)E的一條直線,使得該直線上任一點(diǎn)M與C的連線,都滿足
側(cè)面PAD內(nèi)是否存在過(guò)點(diǎn)E的一條直線,使得該直線上任一點(diǎn)M與C的連線,都滿足![]() 平面BDF,若存在,求出此直線被直線PA、PD所截線段的長(zhǎng)度,若不存在,請(qǐng)明理由.
平面BDF,若存在,求出此直線被直線PA、PD所截線段的長(zhǎng)度,若不存在,請(qǐng)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司有4家直營(yíng)店![]() ,
, ![]() ,
, ![]() ,
, ![]() ,現(xiàn)需將6箱貨物運(yùn)送至直營(yíng)店進(jìn)行銷售,各直營(yíng)店出售該貨物以往所得利潤(rùn)統(tǒng)計(jì)如下表所示.根據(jù)此表,該公司獲得最大總利潤(rùn)的運(yùn)送方式有
,現(xiàn)需將6箱貨物運(yùn)送至直營(yíng)店進(jìn)行銷售,各直營(yíng)店出售該貨物以往所得利潤(rùn)統(tǒng)計(jì)如下表所示.根據(jù)此表,該公司獲得最大總利潤(rùn)的運(yùn)送方式有

A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在矩形ABCD中,AB=4,AD=2,E是CD的中點(diǎn),將△ADE沿AE折起,得到如圖2所示的四棱錐D1—ABCE,其中平面D1AE⊥平面ABCE.
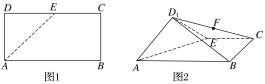
(1)證明:BE⊥平面D1AE;
(2)設(shè)F為CD1的中點(diǎn),在線段AB上是否存在一點(diǎn)M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 是圓錐
是圓錐![]() 的底面
的底面![]() 的直徑,
的直徑,![]() 是圓
是圓![]() 上異于
上異于![]() 的任意一點(diǎn),以
的任意一點(diǎn),以![]() 為直徑的圓與
為直徑的圓與![]() 的另一個(gè)交點(diǎn)為
的另一個(gè)交點(diǎn)為![]() 為
為![]() 的中點(diǎn).現(xiàn)給出以下結(jié)論:
的中點(diǎn).現(xiàn)給出以下結(jié)論:
①![]() 為直角三角形
為直角三角形
②平面![]() 平面
平面![]()
③平面![]() 必與圓錐
必與圓錐![]() 的某條母線平行
的某條母線平行
其中正確結(jié)論的個(gè)數(shù)是
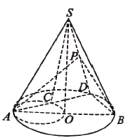
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線C的參數(shù)方程為
中,曲線C的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系中,直線
軸的正半軸為極軸建立極坐標(biāo)系中,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)求C的普通方程和直線![]() 的傾斜角;
的傾斜角;
(Ⅱ)設(shè)點(diǎn)![]() (0,2),
(0,2),![]() 和
和![]() 交于
交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com