【答案】
分析:(Ⅰ)由A與B的度數(shù)求出C的度數(shù),即可求出sinC的值;
(Ⅱ)由正弦定理列出關系式,根據(jù)B表示出C代入計算即可得證;
(Ⅲ)利用平面向量的數(shù)量積運算化簡所求的式子,利用兩角和與差的正弦函數(shù)公式及特殊角的三角函數(shù)值化為一個叫的正弦函數(shù),由B的范圍求出這個角的范圍,利用正弦函數(shù)的圖象與性質(zhì)即可求出范圍.
解答:解:(Ⅰ)sinC=sin(π-A-B)=sin
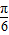
=

;
(Ⅱ)證明:在△ABC中,由正弦定理得
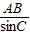
=
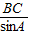
,
∵BC=2,sinA=

,B+C=
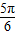
,
∴AB=
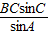
=4sin(
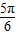
-B);
(Ⅲ)∵|
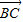
|=2,|
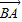
|=4sin(
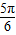
-B),
∴
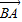
•
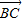
=|
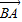
||
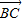
|cosB=8sin(
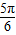
-B)cosB=8cosB(

cosB+
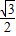
sinB)=4sin(2B+
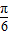
)+2
=2+2cos2B+2
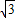
sin2B=4sin(2B+
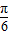
)+2,
∵B∈(
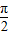
,
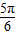
),∴2B+
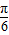
∈(
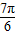
,
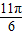
),
∴sin(2B+
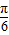
)∈[-1,-

),
則
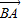
•
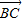
=的取值范圍是[-2,0).
點評:此題考查了正弦定理,平面向量的數(shù)量積運算,兩角和與差的正弦函數(shù)公式,以及正弦函數(shù)的定義域與值域,熟練掌握正弦定理是解本題的關鍵.

 ,
, ,BC=2.
,BC=2. ,求sinC;
,求sinC; ;
; 的取值范圍.
的取值范圍.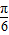 =
= ;
;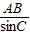 =
=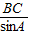 ,
, ,B+C=
,B+C=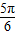 ,
,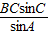 =4sin(
=4sin(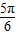 -B);
-B);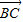 |=2,|
|=2,|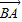 |=4sin(
|=4sin(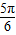 -B),
-B),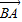 •
•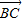 =|
=|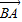 ||
||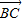 |cosB=8sin(
|cosB=8sin(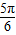 -B)cosB=8cosB(
-B)cosB=8cosB( cosB+
cosB+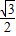 sinB)=4sin(2B+
sinB)=4sin(2B+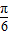 )+2
)+2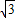 sin2B=4sin(2B+
sin2B=4sin(2B+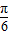 )+2,
)+2,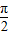 ,
,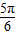 ),∴2B+
),∴2B+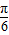 ∈(
∈(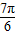 ,
,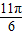 ),
),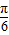 )∈[-1,-
)∈[-1,- ),
),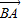 •
•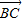 =的取值范圍是[-2,0).
=的取值范圍是[-2,0).

 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案