Question

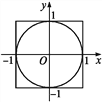
【題目】用隨機模擬的方法估算邊長是2的正方形內切圓的面積(如圖所示),并估計π的近似值.

Answer 1

【答案】見解析；

【解析】試題分析: 隨機模擬的步驟:產生隨機數,統計次數,根據古典概型概率公式計算概率,利用幾何概型概率計算概率,由兩者相等求出π的近似值

試題解析:解:(1)利用計算機產生兩組[0,1]上的均勻隨機數a1,b1.

(2)平移和伸縮變換,a=(a1-0.5)×2,b=(b1-0.5)×2,得到兩組[-1,1]上的均勻隨機數.

(3)統計試驗總次數N和點落在圓內的次數N1(滿足a2+b2≤1的點(a,b)的個數).

(4)計算頻率,即為點落在圓內的概率.

(5)如圖,設圓面積為S,則由幾何概型概率公式得P=.

所以,即S≈,即圓面積的近似值為.

又因為S圓=πr2

點睛:利用隨機模擬的方法計算不規則圖形的面積的一個常用思路是：在不規則圖形外加一個規則圖形，利用幾何概型的概率公式求出落在所求面積的圖形內任意一點的事件發生的概率；再利用隨機模擬的方法產生隨機數，計算相關頻率．當試驗次數增加到一定程度，所得的頻率就可以看成用幾何概型的概率公式求出的概率，進而可求出所求的面積．用類似方法也可求出不規則幾何體的體積．