
 的定義域;
的定義域; )的單調增區間;
)的單調增區間;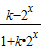 為奇函數,求k的值.
為奇函數,求k的值.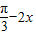 在正弦函數的減區間內求解x的取值范圍即可,最后用區間表示;
在正弦函數的減區間內求解x的取值范圍即可,最后用區間表示;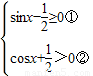 ,
,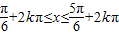 (k∈Z),
(k∈Z),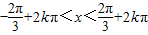 (k∈Z).
(k∈Z).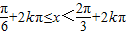 (k∈Z).
(k∈Z).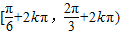 (k∈Z).
(k∈Z).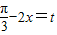 ,
,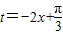 為減函數,
為減函數,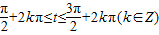 ,
,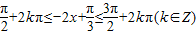 ,
,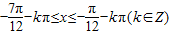 .
.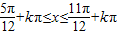 (k∈Z).
(k∈Z).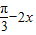 )的單調增區間為:
)的單調增區間為: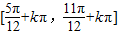 (k∈Z).
(k∈Z).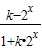 為奇函數,
為奇函數,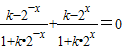 恒成立,
恒成立,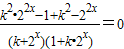 ,
,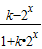 為奇函數的k的值為1或-1.
為奇函數的k的值為1或-1.

 寒假學與練系列答案
寒假學與練系列答案科目:高中數學 來源: 題型:
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
| 1+tanα |
| 1-tanα |
| 2sinα-3cosα |
| 4sinα-9cosα |
查看答案和解析>>
科目:高中數學 來源: 題型:
sinx-
|
| 1 |
| 2 |
| π |
| 3 |
| k-2x |
| 1+k•2x |
查看答案和解析>>
科目:高中數學 來源:2010-2011年浙江省高二下學期期中考試數學2-4 題型:解答題
在棱長為1的正方體 中,
中, 分別是
分別是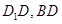 的中點,
的中點,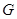 在棱
在棱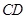 上,且
上,且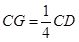 ,H為
,H為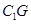 的中點,應用空間向量方法求解下列問題.
的中點,應用空間向量方法求解下列問題.
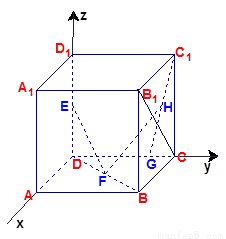
(1)求證: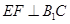 ;
;
(2)求EF與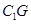 所成的角的余弦;
所成的角的余弦;
(3)求FH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com