
【題目】已知函數f(x)=e1﹣x(﹣a+cosx),a∈R.
(Ⅰ)若函數y=f(x)在[0,π]存在單調增區間,求實數a的取值范圍;
(Ⅱ)若f( ![]() )=0,證明:對于x∈[﹣1,
)=0,證明:對于x∈[﹣1, ![]() ],總有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
],總有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
【答案】解:(I)由題f'(x)=﹣e1﹣x(﹣a+cosx)﹣e1﹣xsinx=﹣e1﹣x(sinx+cosx﹣a),
因為x∈(0,π),函數y=f(x)在[0,π]存在單調增區間,
所以f'(x)=﹣e1﹣x(sinx+cosx﹣a)≥0,
即a≥ ![]() sin(x+
sin(x+ ![]() )在x∈(0,π)恒成立,
)在x∈(0,π)恒成立,
而y=sin(x+ ![]() )在x∈(0,π)的最大值是1,
)在x∈(0,π)的最大值是1,
故a≥ ![]() ;
;
(II)若f( ![]() )=0,則a=0,
)=0,則a=0,
f(﹣x﹣1)=ex+2cos(﹣x﹣1)=ex+2cos(x+1),
而2f'(x)cos(﹣x﹣1)=﹣2e1﹣x(sinx+cosx)cos(x+1),
又因為x∈[﹣1, ![]() ],所以cos(x+1)>0,
],所以cos(x+1)>0,
要證原不等式成立,只要證ex+2﹣2e1﹣x(sinx+cosx)>0,
只要證ex+2>2e1﹣x(sinx+cosx),
只要證e2x+1>2 ![]() sin(x+
sin(x+ ![]() ),在x∈[﹣1,
),在x∈[﹣1, ![]() ]上恒成立,
]上恒成立,
首先構造函數g(x)=2x+2﹣2 ![]() sin(x+
sin(x+ ![]() ),x∈[﹣1,
),x∈[﹣1, ![]() ],
],
因為g′(x)=2﹣2 ![]() cos(x+
cos(x+ ![]() )=2
)=2 ![]() (
( ![]() ﹣cos(x+
﹣cos(x+ ![]() )),
)),
可得,在x∈[﹣1,0]時,g'(x)≤0,即g(x)在[﹣1,0]上是減函數,
在x∈(0, ![]() ]時,g'(x)>0,即g(x)在(0,
]時,g'(x)>0,即g(x)在(0, ![]() ]上是增函數,
]上是增函數,
所以,在[﹣1, ![]() ]上,g(x)min=g(0)=0,所以g(x)≥0,
]上,g(x)min=g(0)=0,所以g(x)≥0,
所以,2 ![]() sin(x+
sin(x+ ![]() )≤2x+2,等號成立當且僅當x=0時,
)≤2x+2,等號成立當且僅當x=0時,
其次構造函數h(x)=e2x+1﹣(2x+2),x∈[﹣1, ![]() ],
],
因為h'(x)=2e2x+1﹣2=2(e2x+1﹣1),
可見x∈[﹣1,﹣ ![]() ]時,h'(x)≤0,即h(x)在[﹣1,﹣
]時,h'(x)≤0,即h(x)在[﹣1,﹣ ![]() ]上是減函數,
]上是減函數,
x∈(﹣ ![]() ,
, ![]() ]時,h'(x)>0,即h(x)在(﹣
]時,h'(x)>0,即h(x)在(﹣ ![]() ,
, ![]() ]上是增函數,
]上是增函數,
所以在[﹣1, ![]() ]上,h(x)min=h(﹣
]上,h(x)min=h(﹣ ![]() )=0,所以h(x)≥0,
)=0,所以h(x)≥0,
所以,e2x+1≥2x+2,等號成立當且僅當x=﹣時.
綜上所述,e2x+1≥2x+2≥2 ![]() sin(x+
sin(x+ ![]() ),
),
因為取等條件并不一致,
所以e2x+1>2 ![]() sin(x+
sin(x+ ![]() ),在x∈[﹣1,
),在x∈[﹣1, ![]() ]上恒成立,
]上恒成立,
所以x∈[﹣1, ![]() ],總有f(﹣x﹣1)+2f'(x)cos(﹣x﹣1)>0成立
],總有f(﹣x﹣1)+2f'(x)cos(﹣x﹣1)>0成立
【解析】(Ⅰ)求出f(x)的導數,根據x的范圍,判斷出f′(x)的符號,從而求出函數的單調性,確定a的范圍即可;(Ⅱ)問題轉化為證明e2x+1>2 ![]() sin(x+
sin(x+ ![]() ),在x∈[﹣1,
),在x∈[﹣1, ![]() ]上恒成立,構造函數g(x)=2x+2﹣2
]上恒成立,構造函數g(x)=2x+2﹣2 ![]() sin(x+
sin(x+ ![]() ),x∈[﹣1,
),x∈[﹣1, ![]() ],求出g(x)的導數,判斷出函數的單調性,從而證出結論.
],求出g(x)的導數,判斷出函數的單調性,從而證出結論.
【考點精析】利用利用導數研究函數的單調性對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 巧學巧練系列答案
巧學巧練系列答案 課課練江蘇系列答案
課課練江蘇系列答案科目:高中數學 來源: 題型:
【題目】函數y=f(x)導函數的圖象如圖所示,則下列說法錯誤的是( )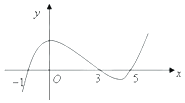
A.(﹣1,3)為函數y=f(x)的遞增區間
B.(3,5)為函數y=f(x)的遞減區間
C.函數y=f(x)在x=0處取得極大值
D.函數y=f(x)在x=5處取得極小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|+|x+1|.
(1)若x∈R,恒有f(x)≥λ成立,求實數λ的取值范圍;
(2)若m∈R,使得m2+2m+f(t)=0成立,試求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列 ![]() 的前n項和為Sn
的前n項和為Sn ![]() ,且滿足:
,且滿足:
① ![]() ;②
;② ![]() ,其中
,其中 ![]() 且
且 ![]() .
.
(1)求p的值;
(2)數列 ![]() 能否是等比數列?請說明理由;
能否是等比數列?請說明理由;
(3)求證:當r ![]() 2時,數列
2時,數列 ![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,a,b,c分別為角A,B,C的對邊,csinC﹣asinA=( ![]() c﹣b)sinB.
c﹣b)sinB.
(Ⅰ)求角A;
(Ⅱ)若a=1,求三角形ABC面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為 ![]() (t為參數)在極坐標系(與直角坐標系xOy取相同的長度單位.且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=6sinθ.
(t為參數)在極坐標系(與直角坐標系xOy取相同的長度單位.且以原點O為極點,以x軸正半軸為極軸)中,圓C的方程為ρ=6sinθ.
(1)求圓C的直角坐標方程;
(2)設圓C與直線l交于點A,B.若點P的坐標為(1,2),求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,底面是邊長為2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O. (Ⅰ)證明:PC⊥BD
(Ⅱ)若E是PA的中點,且△ABC與平面PAC所成的角的正切值為 ![]() ,求二面角A﹣EC﹣B的余弦值.
,求二面角A﹣EC﹣B的余弦值.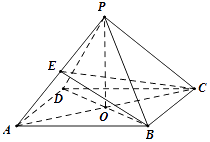
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓E的方程為 ![]() +y2=1(a>1),O為坐標原點,直線l與橢圓E交于點A,B,M為線段AB的中點.
+y2=1(a>1),O為坐標原點,直線l與橢圓E交于點A,B,M為線段AB的中點.
(1)若A,B分別為E的左頂點和上頂點,且OM的斜率為﹣ ![]() ,求E的標準方程;
,求E的標準方程;
(2)若a=2,且|OM|=1,求△AOB面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com