
 如圖所示,在一輕質的杠桿兩端懸掛兩個等質量的實心鐵球和鋁球,杠桿在水平位置平衡,將兩球同時浸沒在水中,則________端下沉,若要杠桿在水平位置再次平衡,應將支點向________端移動(選填“左”或“右”).鐵球的體積為100cm3,當它浸沒在水中靜止時繩子對鐵球的拉力為________N.(ρ鐵=7.9×103kg/m3,取g=10N/kg)
如圖所示,在一輕質的杠桿兩端懸掛兩個等質量的實心鐵球和鋁球,杠桿在水平位置平衡,將兩球同時浸沒在水中,則________端下沉,若要杠桿在水平位置再次平衡,應將支點向________端移動(選填“左”或“右”).鐵球的體積為100cm3,當它浸沒在水中靜止時繩子對鐵球的拉力為________N.(ρ鐵=7.9×103kg/m3,取g=10N/kg)

科目:初中物理 來源: 題型:
 如圖所示,有一輕質木板OA能繞O點轉動,A端系細繩懸掛于墻上B點,并使A端上翹.在靠近A端處放著一小球,在小球沿木板滾下的過程中,細繩對木板的拉力將( )
如圖所示,有一輕質木板OA能繞O點轉動,A端系細繩懸掛于墻上B點,并使A端上翹.在靠近A端處放著一小球,在小球沿木板滾下的過程中,細繩對木板的拉力將( )查看答案和解析>>
科目:初中物理 來源: 題型:
 如圖所示,在一輕質的杠桿兩端懸掛兩個等質量的實心鐵球和鋁球,杠桿在水平位置平衡,將兩球同時浸沒在水中,則
如圖所示,在一輕質的杠桿兩端懸掛兩個等質量的實心鐵球和鋁球,杠桿在水平位置平衡,將兩球同時浸沒在水中,則查看答案和解析>>
科目:初中物理 來源: 題型:
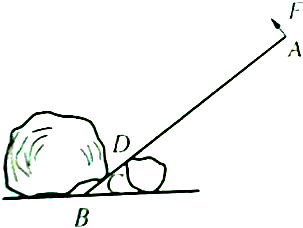 如圖所示,有一輕質杠桿總長為1m,其中BC=CD=10cm,在力F的作用下,石頭上的C點沿垂直于杠桿的方向移動了2cm,設力F的大小為100N,方向垂直于杠桿AB向上,則力F至少做了多少功?
如圖所示,有一輕質杠桿總長為1m,其中BC=CD=10cm,在力F的作用下,石頭上的C點沿垂直于杠桿的方向移動了2cm,設力F的大小為100N,方向垂直于杠桿AB向上,則力F至少做了多少功?查看答案和解析>>
科目:初中物理 來源:2011年湖南省長沙市中考物理模擬試卷(六)(解析版) 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com