
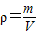 求出石塊的密度.
求出石塊的密度.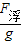 =
=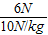 =0.6kg,
=0.6kg,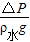 =
=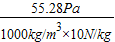 =5.528×10-3m,
=5.528×10-3m,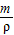
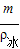 -
-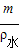 =S×h降,
=S×h降,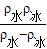 =100×10-4m2×5.528×10-3m×
=100×10-4m2×5.528×10-3m× =0.49752kg,
=0.49752kg, =6×10-4m3-
=6×10-4m3-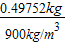 =4.72×10-5m3,
=4.72×10-5m3,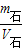 =
= =2.17×103kg/m3.
=2.17×103kg/m3.

 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:初中物理 來源: 題型:
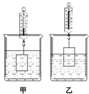 (2013?延慶縣一模)底面積為 100cm 的燒杯中裝有適量水.當金屬塊浸沒在水中靜止時,如圖甲所示,彈簧測力計的示數 F1=3.4N,水對杯底的壓強為 P1;當金屬塊總體積的
(2013?延慶縣一模)底面積為 100cm 的燒杯中裝有適量水.當金屬塊浸沒在水中靜止時,如圖甲所示,彈簧測力計的示數 F1=3.4N,水對杯底的壓強為 P1;當金屬塊總體積的| 1 |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com