

 =
= =100Ω,
=100Ω, =
= =400Ω,
=400Ω, =
= =1.15×105J,
=1.15×105J,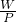 =
= =
= ≈238s;
≈238s;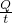 =
= =440W;
=440W; =
= =110Ω.
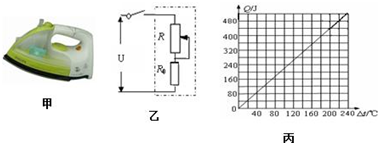
=110Ω.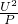 可以求出電阻R0及R的阻值.
可以求出電阻R0及R的阻值.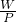 求出電熨斗的預熱時間.
求出電熨斗的預熱時間.

 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中物理 來源: 題型:

查看答案和解析>>
科目:初中物理 來源: 題型:
查看答案和解析>>
科目:初中物理 來源:2012年江蘇省揚州市寶應縣中考物理模擬試卷(二)(解析版) 題型:解答題

查看答案和解析>>
科目:初中物理 來源:2011年江蘇省揚州市儀征市中考物理一模試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中物理 來源:2012年湖北省黃岡市中考適應性考試物理試卷(6月份)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com