
科目: 來源: 題型:
【題目】某生產商存有1200千克![]() 產品,生產成本為150元/千克,售價為400元千克.因市場變化,準備低價一次性處理掉部分存貨,所得貨款全部用來生產
產品,生產成本為150元/千克,售價為400元千克.因市場變化,準備低價一次性處理掉部分存貨,所得貨款全部用來生產![]() 產品,
產品,![]() 產品售價為200元/千克.經市場調研發現,
產品售價為200元/千克.經市場調研發現,![]() 產品存貨的處理價格
產品存貨的處理價格![]() (元/千克)與處理數量
(元/千克)與處理數量![]() (千克)滿足一次函數關系(
(千克)滿足一次函數關系(![]() ),且得到表中數據.
),且得到表中數據.
|
|
200 | 350 |
400 | 300 |
(1)請求出處理價格![]() (元千克)與處理數量
(元千克)與處理數量![]() (千克)之間的函數關系;
(千克)之間的函數關系;
(2)若![]() 產品生產成本為100元千克,
產品生產成本為100元千克,![]() 產品處理數量為多少千克時,生產
產品處理數量為多少千克時,生產![]() 產品數量最多,最多是多少?
產品數量最多,最多是多少?
(3)由于改進技術,![]() 產品的生產成本降低到了
產品的生產成本降低到了![]() 元/千克,設全部產品全部售出,所得總利潤為
元/千克,設全部產品全部售出,所得總利潤為![]() (元),若
(元),若![]() 時,滿足
時,滿足![]() 隨
隨![]() 的增大而減小,求
的增大而減小,求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目: 來源: 題型:
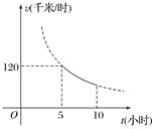
【題目】一輛客車從甲地出發前往乙地,平均速度v(千米/小時)與所用時間t(小時)的函數關系如圖所示,其中60≤v≤120.
(1)直接寫出v與t的函數關系式;
(2)若一輛貨車同時從乙地出發前往甲地,客車比貨車平均每小時多行駛20千米,3小時后兩車相遇.
①求兩車的平均速度;
②甲、乙兩地間有兩個加油站A、B,它們相距200千米,當客車進入B加油站時,貨車恰好進入A加油站(兩車加油的時間忽略不計),求甲地與B加油站的距離.
查看答案和解析>>
科目: 來源: 題型:
【題目】小明在一次打籃球時,籃球傳出后的運動路線為如圖所示的拋物線,以小明所站立的位置為原點O建立平面直角坐標系,籃球出手時在O點正上方1m處的點P.已知籃球運動時的高度y(m)與水平距離x(m)之間滿足函數表達式y=-![]() x2+x+c.
x2+x+c.
(1)求y與x之間的函數表達式;
(2)球在運動的過程中離地面的最大高度;
(3)小亮手舉過頭頂,跳起后的最大高度為BC=2.5m,若小亮要在籃球下落過程中接到球,求小亮離小明的最短距離OB.

查看答案和解析>>
科目: 來源: 題型:
【題目】某公司計劃投入50萬元,開發并生產甲乙兩種產品,根據市場調查預計甲產品的年獲利y1(萬元)與投入資金x(萬元)成正比例,乙產品的年獲利y2(萬元)與投入資金x(萬元)的平方成正比例,設該公司投入乙產品x(萬元),兩種產品的年總獲利為y萬元(x≥0),得到了表中的數據.
x(萬元) | 20 | 30 |
y(萬元) | 10 | 13 |
(1)求y與x的函數關系式;
(2)該公司至少可獲得多少利潤?請你利用所學的數學知識對該公司投入資金的分配提出合理化建
議,使他能獲得最大利潤,并求出最大利潤是多少?
(3)若從年總利潤扣除投入乙產品資金的a倍(a≤1)后,剩余利潤隨x增大而減小,求a的取值
范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】例 如圖①,李老師設計了一個探究杠桿平衡條件的實驗:在一個自制的類似天平的儀器的左邊固定托盤![]() 中放置一個重物,在右邊活動托盤
中放置一個重物,在右邊活動托盤![]() (可左右移動)中放置一定質量的砝碼,使得儀器左右平衡.改變活動托盤
(可左右移動)中放置一定質量的砝碼,使得儀器左右平衡.改變活動托盤![]() 與點
與點![]() 的距離
的距離![]() ,觀察活動托盤
,觀察活動托盤![]() 中砝碼的質量
中砝碼的質量![]() 的變化情況.實驗數據記錄如表:
的變化情況.實驗數據記錄如表:
| 10 | 15 | 20 | 25 | 30 |
| 30 | 20 | 15 | 12 | 10 |
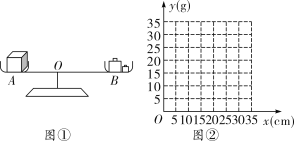
(1)把表中![]() 的各組對應值作為點的坐標,在圖②的坐標系中描出相應的點,用平滑曲線連接這些點;
的各組對應值作為點的坐標,在圖②的坐標系中描出相應的點,用平滑曲線連接這些點;
(2)觀察所畫的圖象,猜測![]() 與
與![]() 之間的函數關系,求出函數關系式;
之間的函數關系,求出函數關系式;
(3)當砝碼的質量為![]() 時,活動托盤
時,活動托盤![]() 與點
與點![]() 的距離是多少?
的距離是多少?
查看答案和解析>>
科目: 來源: 題型:
【題目】某校準備組織師生共60人,從甲地乘動車前往乙地參加夏令營活動,動車票價格如表所示:(教師按成人票價購買,學生按學生票價購買).
運行區間 | 成人票價(元/張) | 學生票價(元/張) | ||
出發站 | 終點站 | 一等座 | 二等座 | 二等座 |
甲地 | 乙地 | 26 | 22 | 16 |
若師生均購買二等座票,則共需1020元.
(1)求參加活動的教師和學生各有多少人?
(2)由于部分教師需提早前往做準備工作,這部分教師均購買一等座票,后續前往的教師和學生均購買二等座票.設提早前往的教師有![]() 人,購買一、二等座票全部費用為
人,購買一、二等座票全部費用為![]() 元.
元.
①求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
②若購買一、二等座票全部費用不多于1030元,則提早前往的教師最多只能有多少人?
查看答案和解析>>
科目: 來源: 題型:
【題目】某汽車租賃公司對某款汽車的租賃方式按時段計費,該公司要求租賃方必須在9天內(包括9天)將所租汽車歸還.租賃費用![]() (元)隨時間
(元)隨時間![]() (天)的變化圖象為折線
(天)的變化圖象為折線![]() ,如圖所示.
,如圖所示.
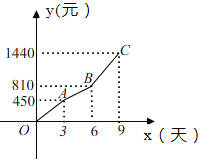
(1)當租賃時間不超過3天時,求每日租金.
(2)當![]() 時,求
時,求![]() (元)與
(元)與![]() (天)的函數關系式.
(天)的函數關系式.
(3)甲、乙兩人租賃該款汽車各一輛,兩人租賃的時間共為9天,甲租的天數少于3天,乙比甲多支付費用720元.請問乙租這款汽車多長時間?
查看答案和解析>>
科目: 來源: 題型:
【題目】在面積都相等的所有矩形中,當其中一個矩形的一邊長為1時,它的另一邊長為3.
(1)設矩形的相鄰兩邊長分別為x,y.
①求y關于x的函數表達式;
②當y≥3時,求x的取值范圍;
(2)圓圓說其中有一個矩形的周長為6,方方說有一個矩形的周長為10,你認為圓圓和方方的說法對嗎?為什么?
查看答案和解析>>
科目: 來源: 題型:
【題目】某新建小區要修一條1050米長的路,甲、乙兩個工程隊想承建這項工程.經
了解得到以下信息(如表):
工程隊 | 每天修路的長度(米) | 單獨完成所需天數(天) | 每天所需費用(元) |
甲隊 | 30 | n | 600 |
乙隊 | m | n﹣14 | 1160 |
(1)甲隊單獨完成這項工程所需天數n= ,乙隊每天修路的長度m= (米);
(2)甲隊先修了x米之后,甲、乙兩隊一起修路,又用了y天完成這項工程(其中x,y為正整數).
①當x=90時,求出乙隊修路的天數;
②求y與x之間的函數關系式(不用寫出x的取值范圍);
③若總費用不超過22800元,求甲隊至少先修了多少米.
查看答案和解析>>
科目: 來源: 題型:
【題目】![]() ,
,![]() 兩地相距
兩地相距![]() .甲、乙兩人都由
.甲、乙兩人都由![]() 地去
地去![]() 地,甲騎自行車,平均速度為
地,甲騎自行車,平均速度為![]() ;乙乘汽車,平均速度為
;乙乘汽車,平均速度為![]() ,且比甲晚
,且比甲晚![]() 出發.設甲的騎行時間為
出發.設甲的騎行時間為![]() .
.
(1)根據題意,填寫下表:
時間 與 | 0.5 | 1.8 | ______ |
甲與 | 5 | ______ | 20 |
乙與 | 0 | 12 | ______ |
(2)設甲,乙兩人與![]() 地的距離為
地的距離為![]() 和
和![]() ,寫出
,寫出![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)設甲,乙兩人之間的距離為![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com