相關習題
0 159787 159795 159801 159805 159811 159813 159817 159823 159825 159831 159837 159841 159843 159847 159853 159855 159861 159865 159867 159871 159873 159877 159879 159881 159882 159883 159885 159886 159887 159889 159891 159895 159897 159901 159903 159907 159913 159915 159921 159925 159927 159931 159937 159943 159945 159951 159955 159957 159963 159967 159973 159981 366461
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:填空題
若關于x的一元二次方程x2-2x+m=0有實數根,則m的取值范圍是 .
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:填空題
如圖,平行四邊形ABCD的周長為16cm,AC,BD相交于點O,OE⊥AC于O,則△DCE的周長為
cm.
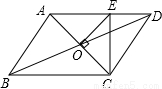
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:填空題
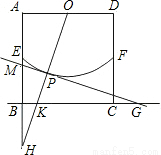
如圖在邊長為2的正方形ABCD中,E,F,O分別是AB,CD,AD的中點,以O為圓心,以OE為半徑畫弧EF.P是
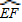
上的一個動點,連接OP,并延長OP交線段BC于點K,過點P作⊙O的切線,分別交射線AB于點M,交直線BC于點G.若
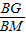
=3,則BK=
.
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
計算:
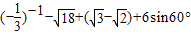
.
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
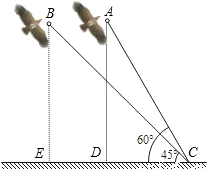
在一個陽光明媚、清風徐來的周末,小明和小強一起到郊外放風箏﹒他們把風箏放飛后,將兩個風箏的引線一端都固定在地面上的C處(如圖).現已知風箏A的引線(線段AC)長20m,風箏B的引線(線段BC)長24m,在C處測得風箏A的仰角為60°,風箏B的仰角為45°.
(1)試通過計算,比較風箏A與風箏B誰離地面更高?
(2)求風箏A與風箏B的水平距離.(精確到0.01m;參考數據:sin45°≈0.707,cos45°≈0.707,tan45°=1,sin60°≈0.866,cos60°=0.5,tan60°≈1.732)
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
某種電腦病毒傳播非常快,如果一臺電腦被感染,經過兩輪感染后就會有81臺電腦被感染.請你用學過的知識分析,每輪感染中平均一臺電腦會感染幾臺電腦?若病毒得不到有效控制,3輪感染后,被感染的電腦會不會超過700臺?
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
上海大學青年志愿者協會對報名參加2010年上海世博會志愿者選拔活動的學生進行了一次與大運知識有關的測試,小亮對自己班有報名參加測試的同學的測試成績作了適當的處理,將成績分成三個等級:一般、良好、優秀,并將統計結果繪成了如下兩幅不完整的統計圖,請你根據圖中所給信息解答下列問題:
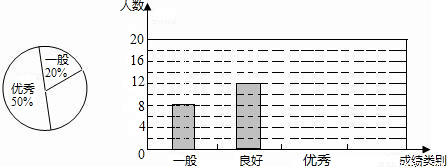
(1)請將兩幅統計圖補充完整;
(2)小亮班共有______名學生參加了這次測試,如果青年志愿者協會決定讓成績為“優秀”的學生參加下一輪的測試,那么小亮班有______人將參加下輪測試;
(3)若這所高校共有1200名學生報名參加了這次志愿者選拔活動的測試,請以小亮班的測試成績的統計結果來估算全校共有多少名學生可以參加下一輪的測試.
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
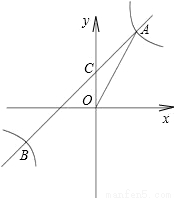
如圖,反比例函數y=
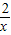
的圖象與一次函數y=kx+b的圖象交于點A(m,2),點B(-2,n),一次函數圖象與y軸的交點為C.
(1)求一次函數解析式;
(2)求C點的坐標;
(3)求△AOC的面積.
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
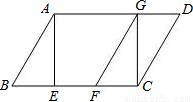
已知:如圖,在平行四邊形ABCD中,AE是BC邊上的高,將△ABE沿BC方向平移,使點E與點C重合,得△GFC.
(1)求證:BE=DG;
(2)若∠B=60°,當AB與BC滿足什么數量關系時,四邊形ABFG是菱形?證明你的結論.
查看答案和解析>>
科目:
來源:2012年湖北省襄陽市南漳縣九集中學中考數學一模試卷(解析版)
題型:解答題
某汽車制造廠開發了一款新式電動汽車,計劃一年生產安裝240輛.由于抽調不出足夠的熟練工來完成新式電動汽車的安裝,工廠決定招聘一些新工人;他們經過培訓后上崗,也能獨立進行電動汽車的安裝.生產開始后,調研部門發現:1名熟練工和2名新工人每月可安裝8輛電動汽車;2名熟練工和3名新工人每月可安裝14輛電動汽車.
(1)每名熟練工和新工人每月分別可以安裝多少輛電動汽車?
(2)如果工廠招聘n(0<n<10)名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一年的安裝任務,那么工廠有哪幾種新工人的招聘方案?
(3)在(2)的條件下,工廠給安裝電動汽車的每名熟練工每月發2000元的工資,給每名新工人每月發1200元的工資,那么工廠應招聘多少名新工人,使新工人的數量多于熟練工,同時工廠每月支出的工資總額W(元)盡可能地少?
查看答案和解析>>


 如圖在邊長為2的正方形ABCD中,E,F,O分別是AB,CD,AD的中點,以O為圓心,以OE為半徑畫弧EF.P是
如圖在邊長為2的正方形ABCD中,E,F,O分別是AB,CD,AD的中點,以O為圓心,以OE為半徑畫弧EF.P是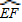 上的一個動點,連接OP,并延長OP交線段BC于點K,過點P作⊙O的切線,分別交射線AB于點M,交直線BC于點G.若
上的一個動點,連接OP,并延長OP交線段BC于點K,過點P作⊙O的切線,分別交射線AB于點M,交直線BC于點G.若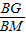 =3,則BK= .
=3,則BK= .

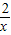 的圖象與一次函數y=kx+b的圖象交于點A(m,2),點B(-2,n),一次函數圖象與y軸的交點為C.
的圖象與一次函數y=kx+b的圖象交于點A(m,2),點B(-2,n),一次函數圖象與y軸的交點為C.
