相關習題
0 157887 157895 157901 157905 157911 157913 157917 157923 157925 157931 157937 157941 157943 157947 157953 157955 157961 157965 157967 157971 157973 157977 157979 157981 157982 157983 157985 157986 157987 157989 157991 157995 157997 158001 158003 158007 158013 158015 158021 158025 158027 158031 158037 158043 158045 158051 158055 158057 158063 158067 158073 158081 366461
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:填空題
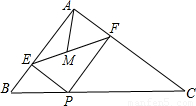
在△ABC中,AB=6,AC=8,BC=10,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為
.
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:填空題
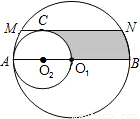
如圖,AB是⊙O
1的直徑,AO
1是⊙O
2的直徑,弦MN∥AB,且MN與⊙O
2相切于C點,若⊙O
1的半徑為2,則O
1B、
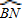
、NC與
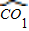
所圍成的陰影部分的面積是
.
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
先化簡,再求值:
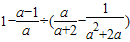
,其中x=
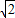
-1.
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
一個不透明的布袋里裝有4個大小、質地均相同的乒乓球,每個球上面分別標有1,2,3,4,小林先從布袋中隨機抽取一個乒乓球(不放回去),再從剩下的3個球中隨機抽取第二個乒乓球.
(1)請你列出所有可能的結果;
(2)求兩次取得乒乓球的數字之積為奇數的概率.
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
如圖,小明在樓上點A處觀察旗桿BC,測得旗桿頂部B的仰角為30°,測得旗桿底部C的俯角為60°,已知點A距地面的高AD為12m.求旗桿的高度.

查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
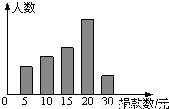
某校學生會干部對校學生會倡導的“助殘”自愿捐款活動進行抽樣調查,得到一組學生捐款情況的數據,下圖是根據這組數據繪制的統計圖,圖中從左到右各長方形高度之比為3:4:5:8:2,又知此次調查中捐15元和20元的人數共39人.
(1)他們一共抽查了多少人捐款數不少于20元的概率是多少?
(2)這組數據的眾數、中位數各是多少?
(3)若該校共有2310名學生,請估算全校學生共捐款多少元?
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
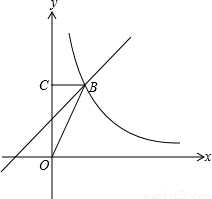
如圖所示一次函數y=x+b與反比例函數
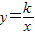
在第一象限的圖象交于點B,且點B的橫坐標為1,過點B作y軸的垂線,C為垂足,若S
△BCO=

,求一次函數和反比例函數的解析式.
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
如圖,已知△ABC是等邊三角形,D、E分別在邊BC、AC上,且CD=CE,連接DE并延長至點F,使EF=AE,連接AF、BE和CF.
(1)求證:△BCE≌△FDC;
(2)判斷四邊形ABDF是怎樣的四邊形,并說明理由.

查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
某汽車制造廠開發了一款新式電動汽車,計劃一年生產安裝240輛.由于抽調不出足夠的熟練工來完成新式電動汽車的安裝,工廠決定招聘一些新工人;他們經過培訓后上崗,也能獨立進行電動汽車的安裝.生產開始后,調研部門發現:1名熟練工和2名新工人每月可安裝8輛電動汽車;2名熟練工和3名新工人每月可安裝14輛電動汽車.
(1)每名熟練工和新工人每月分別可以安裝多少輛電動汽車?
(2)如果工廠招聘n(0<n<10)名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一年的安裝任務,那么工廠有哪幾種新工人的招聘方案?
(3)在(2)的條件下,工廠給安裝電動汽車的每名熟練工每月發2000元的工資,給每名新工人每月發1200元的工資,那么工廠應招聘多少名新工人,使新工人的數量多于熟練工,同時工廠每月支出的工資總額W(元)盡可能地少?
查看答案和解析>>
科目:
來源:2012年湖北省襄樊市襄城區中考數學模擬試卷(解析版)
題型:解答題
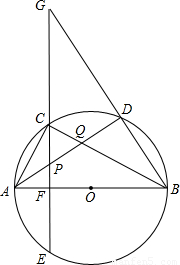
已知:如圖,△ABC內接于⊙O,AB為直徑,弦CE⊥AB于F,C是
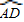
的中點,連接BD并延長交EC的延長線于點G,連接AD,分別交CE、BC于點P、Q.
(1)求證:P是△ACQ的外心;
(2)若
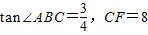
,求CQ的長;
(3)求證:(FP+PQ)
2=FP•FG.
查看答案和解析>>


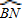 、NC與
、NC與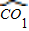 所圍成的陰影部分的面積是 .
所圍成的陰影部分的面積是 .


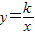 在第一象限的圖象交于點B,且點B的橫坐標為1,過點B作y軸的垂線,C為垂足,若S△BCO=
在第一象限的圖象交于點B,且點B的橫坐標為1,過點B作y軸的垂線,C為垂足,若S△BCO= ,求一次函數和反比例函數的解析式.
,求一次函數和反比例函數的解析式.

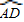 的中點,連接BD并延長交EC的延長線于點G,連接AD,分別交CE、BC于點P、Q.
的中點,連接BD并延長交EC的延長線于點G,連接AD,分別交CE、BC于點P、Q.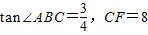 ,求CQ的長;
,求CQ的長;