
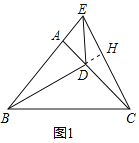
【題目】如圖1,在![]() 和
和![]() 中
中![]() ,
,![]() ,
,![]() ,連接
,連接![]() ,
,![]() ,
,![]() 繞點
繞點![]() 自由旋轉.
自由旋轉.

(1)當![]() 在
在![]() 邊上時,
邊上時,
①線段![]() 和線段
和線段![]() 的關系是____________________;
的關系是____________________;
②若![]() ,則
,則![]() 的度數為____________;
的度數為____________;
(2)如圖2,點![]() 不在
不在![]() 邊上,
邊上,![]() ,
,![]() 相交于點
相交于點![]() ,(l)問中的線段
,(l)問中的線段![]() 和線段
和線段![]() 的關系是否仍然成立?并說明理由.
的關系是否仍然成立?并說明理由.
【答案】(1)①BD=CE,BD⊥CE,②67.5°;(2)(1)問中的線段BD和線段CE的關系仍然成立
【解析】
(1)①延長BD交CE于H,證明△ABD≌△ACE,根據全等三角形的性質得到BD=CE,∠ABD=∠ACE,求出∠CHD=90°,得到BD⊥CE,得到答案;
②根據等腰三角形的性質得到∠ABC=∠ACB=45°,根據等腰三角形的性質、三角形的外角性質計算即可;
(2)仿照(1)①的作法證明即可.
解:(1)①延長BD交CE于H,
在△ABD和△ACE中,
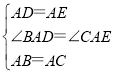
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠ADB=90°,∠ADB=∠CDH,
∴∠DCH+∠CDH=90°,即∠CHD=90°,
∴BD⊥CE,
故答案為:BD=CE,BD⊥CE;
②BC=AD+AB=AE+AB=BE,
∴∠BEC=∠BCE,
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∴∠BEC=∠BCE=67.5°,
∵BE=BC,BH⊥CE,
∴∠CBH=∠EBH=∠ACE,
∴∠ADB=∠DBC+∠DCB=∠ACE+∠DCB=67.5°,
故答案為:67.5°;
(2)(1)問中的線段BD和線段CE的關系仍然成立,
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE
理由如下:在△ABD和△ACE中,
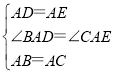
∴△ABD≌△ACE(SAS)
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠ANB=90°,∠ANB=∠FNC,
∴∠ACF+∠DNC=90°,即∠CFN=90°,
∴BD⊥CE,
綜上所述,BD=CE,BD⊥CE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知:直線AB∥CD,點E. F分別是AB、CD上的點。
(1)如圖1,當點P在AB、CD內部時,試說明:∠EPF=∠AEP+∠CFP;
(2)如圖2,當點P在AB上方時,∠EPF、∠AEP、∠CFP之間有怎樣的數量關系?并說明理由。


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸、y軸分別交于點B、點C,經過B、C兩點的拋物線
與x軸、y軸分別交于點B、點C,經過B、C兩點的拋物線![]() 與x軸的另一個交點為A,頂點為P.
與x軸的另一個交點為A,頂點為P.

(1)求該拋物線的解析式;
(2)連接AC,在x軸上是否存在點Q,使以P、B、Q為頂點的三角形與△ABC相似?若存在,請求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校鍋爐旁建有一個儲煤庫,開學初購進一批煤,現在知道:按每天用煤0.6噸計算,一學期(按150天計算)剛好用完.若每天的耗煤量為 x噸,那么這批煤能維持 y天.
(1)則 y與 x之間有怎樣的函數關系?
(2)畫出此函數的圖象.
(3)若每天節約0.1噸,則這批煤能多維持多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y1=﹣![]() x2+bx+c的圖象與x軸、y軸分別交于點A(﹣1,0)和點B(0,2),圖象的對稱軸交x軸于點C,一次函數y2=mx+n的圖象經過點B、C.
x2+bx+c的圖象與x軸、y軸分別交于點A(﹣1,0)和點B(0,2),圖象的對稱軸交x軸于點C,一次函數y2=mx+n的圖象經過點B、C.
(1)求二次函數的解析式y1和一次函數的解析式y2;
(2)點P在x軸下方的二次函數圖象上,且S△ACP=33,求點P的坐標;
(3)結合圖象,求當x取什么范圍的值時,有y1≤y2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,每個圖案都由若干個“●”組成,其中第①個圖案中有7個“●”,第②個圖案中有13個“●”,…,則第⑨個圖案中“●”的個數為( )

A.87B.91C.103D.111
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ABC=90°,D是BC的中點,E是AD的中點,過點A作AF∥BC交BE的延長線于點F.
(1)證明四邊形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】模具廠計劃生產面積為4,周長為m的矩形模具.對于m的取值范圍,小亮已經能用“代數”的方法解決,現在他又嘗試從“圖形”的角度進行探究,過程如下:
(1)建立函數模型
設矩形相鄰兩邊的長分別為x,y,由矩形的面積為4,得![]() ,即
,即![]() ;由周長為m,得
;由周長為m,得![]() ,即
,即![]() .滿足要求的
.滿足要求的![]() 應是兩個函數圖象在第 象限內交點的坐標.
應是兩個函數圖象在第 象限內交點的坐標.
(2)畫出函數圖象
函數![]() 的圖象如圖所示,而函數
的圖象如圖所示,而函數![]() 的圖象可由直線
的圖象可由直線![]() 平移得到.請在同一直角坐標系中直接畫出直線
平移得到.請在同一直角坐標系中直接畫出直線![]() .
.
(3)平移直線![]() ,觀察函數圖象
,觀察函數圖象
①當直線平移到與函數![]() 的圖象有唯一交點
的圖象有唯一交點![]() 時,周長m的值為 ;
時,周長m的值為 ;
②在直線平移過程中,交點個數還有哪些情況?請寫出交點個數及對應的周長m的取值范圍.
(4)得出結論
若能生產出面積為4的矩形模具,則周長m的取值范圍為 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com