
【題目】拋物線![]() (
(![]() ,
,![]() ,
,![]() 為常數,且
為常數,且![]() )經過點
)經過點![]() 和
和![]() ,且
,且![]() ,當
,當![]() 時,
時,![]() 隨著
隨著![]() 的增大而減小.下列結論:①
的增大而減小.下列結論:①![]() ;②若點
;②若點![]() ,點
,點![]() 都在拋物線上,則
都在拋物線上,則![]() ;③
;③![]() ;④若
;④若![]() ,則
,則![]() .其中結論正確的個數是( )
.其中結論正確的個數是( )
A.1個B.2個C.3個D.4個
【答案】B
【解析】
利用x<-1時,y隨著x的增大而減小可判斷拋物線開口向上,則a>0,由于拋物線經過點(-1,0)和(m,0),且1<m<2,可判斷拋物線的對稱軸的位置,所以![]() ,于是可對①進行判斷;
,于是可對①進行判斷;
通過比較點A到對稱軸的距離和點B到對稱軸的距離可對②進行判斷;
根據二次函數圖象上點的坐標特征得到a-b+c=0,am2+bm+c=0,消去c,再因式分解得到(m+1)(m-1)+b(m-1)=0,于是可對③進行判斷;
利用拋物線頂點的縱坐標小于-1得到![]() ,然后利用不等式性質變形后可對④進行判斷.
,然后利用不等式性質變形后可對④進行判斷.
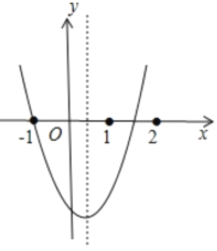
∵拋物線過點![]() ,當
,當![]() 時,
時,![]() 隨著
隨著![]() 的增大而減小,
的增大而減小,
∴拋物線開口向上.∴![]() .
.
∵拋物線經過點![]() 和
和![]() ,且
,且![]() ,
,
∴![]() .∴
.∴![]() .故①正確;
.故①正確;
∵點![]() ,點
,點![]() 都在拋物線上,而點
都在拋物線上,而點![]() 到對稱軸的距離比點
到對稱軸的距離比點![]() 到對稱軸
到對稱軸
的距離要大,
∴![]() .故②錯誤;
.故②錯誤;
∵拋物線經過點![]() 和
和![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .故③正確;
.故③正確;
∵![]() ,∴
,∴![]() .又
.又![]() ,
,
∴![]() .故④錯誤.
.故④錯誤.
故選B.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,支付方式的“眾數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
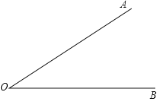
【題目】下面是小華設計的“作一個角等于已知角的2倍”的尺規作圖過程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如圖,
①在射線![]() 上任取一點
上任取一點![]() ;
;
②作線段![]() 的垂直平分線,交
的垂直平分線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ;
;
③連接![]() ;
;
所以![]() 即為所求作的角.
即為所求作的角.
根據小華設計的尺規作圖過程,
(1)使用直尺和圓規補全圖形(保留作圖痕跡);
(2)完成下面的證明(說明:括號里填寫推理的依據).
證明:∵![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,經過原點O的拋物線![]() (a≠0)與x軸交于另一點A(
(a≠0)與x軸交于另一點A(![]() ,0),在第一象限內與直線y=x交于點B(2,t).
,0),在第一象限內與直線y=x交于點B(2,t).
(1)求這條拋物線的表達式;
(2)在第四象限內的拋物線上有一點C,滿足以B,O,C為頂點的三角形的面積為2,求點C的坐標;
(3)如圖2,若點M在這條拋物線上,且∠MBO=∠ABO,在(2)的條件下,是否存在點P,使得△POC∽△MOB?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽市精準扶貧工作已進入攻堅階段.貧困戶張大爺在某單位的幫扶下,把一片坡地改造后種植了優質水果藍莓,今年正式上市銷售.在銷售的30天中,第一天賣出20千克,為了擴大銷量,采取了降價措施,以后每天比前一天多賣出4千克.第x天的售價為y元/千克,y關于x的函數解析式為![]() 且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
(1)m= ,n= ;
(2)求銷售藍莓第幾天時,當天的利潤最大?最大利潤是多少?
(3)在銷售藍莓的30天中,當天利潤不低于870元的共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]()
![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,
,![]() ,與
,與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,
上一點,![]() 于點
于點![]() ,
,![]() 軸交拋物線于點
軸交拋物線于點![]() .
.
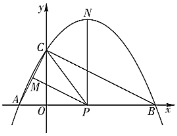
(1)求二次函數![]() 的解析式;
的解析式;
(2)①當![]() 為等腰三角形時,求點
為等腰三角形時,求點![]() 的坐標;
的坐標;
②求![]() 的最大值;
的最大值;
(3)直接寫出當![]() 面積最大時,點
面積最大時,點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場經營一批進價為2元的小商品,在市場營銷中發現日銷售單價x元與日銷售量y件有如下關系:
x | 3 | 5 | 9 | 11 |
y | 18 | 14 | 6 | 2 |
(1)預測此商品日銷售單價為11.5元時的日銷售量;
(2)設經營此商品日銷售利潤(不考慮其他因素)為P元,根據銷售規律,試求日銷售利潤P元與銷售單價x元之間的函數關系式,問日銷售利潤P是否存在最大值或最小值?若有,試求出;若無,請說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:
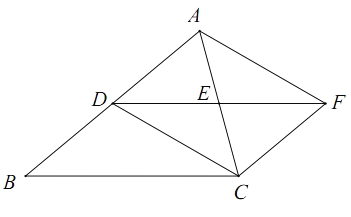
【題目】如圖,在△ABC中,D為AB中點,過點D作DF//BC交AC于點E,且DE=EF,連接AF,CF,CD.
(1)求證:四邊形ADCF為平行四邊形;
(2)若∠ACD=45°,∠EDC=30°,BC=4,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C、E在⊙O上,∠B=2∠ACE,在BA的延長線上有一點P,使得∠P=∠BAC,弦CE交AB于點F,連接AE.
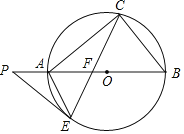
(1)求證:PE是⊙O的切線;
(2)若AF=2,AE=EF=![]() ,求OA的長.
,求OA的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com