
【題目】如圖,已知點![]() 、
、![]() 在雙曲線
在雙曲線![]()
![]() 上,
上,![]() 軸于
軸于![]() ,
,![]() 軸于點
軸于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 是
是![]() 的中點.
的中點.
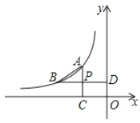
(1)試判斷四邊形![]() 的形狀,并說明理由.
的形狀,并說明理由.
(2)若![]() 的面積為
的面積為![]() ,求該雙曲線的解析式.
,求該雙曲線的解析式.
【答案】(1)菱形,理由見解析;(2)![]() .
.
【解析】
(1)連接AD、CD、BC;AC⊥x軸于C,BD⊥y軸于點D,則AC⊥BD;設A(m,n),則mn=k,P(m,![]() n),再確定B點坐標,進而說明PD=PB,AP=PC, 即可判定四邊形ABCD為菱形;
n),再確定B點坐標,進而說明PD=PB,AP=PC, 即可判定四邊形ABCD為菱形;
(2)由△ABP的面積為3,知BP![]() AP=6.由反比例函數
AP=6.由反比例函數![]() 中k的幾何意義,知本題k=OC
中k的幾何意義,知本題k=OC![]() AC,再由反比例函數的性質以及P是AC的中點的條件,得出OC=BP,AC=2AP,從而完成解答.
AC,再由反比例函數的性質以及P是AC的中點的條件,得出OC=BP,AC=2AP,從而完成解答.
解:(1) 四邊形ABCD為菱形,理由如下:
如圖:連接AD、CD、BC;AC⊥x軸于C,BD⊥y軸于點D,
∴AC⊥BD;
設A(m,n),則mn=k,P(m,![]() n),
n),
B點縱坐標為![]() n,橫坐標為
n,橫坐標為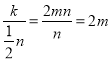 ,
,
∴PD=PB,
又∵AP=PC,
∴四邊形ABCD是菱形;
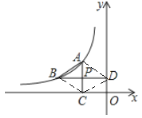
(2)∵△ABP的面積為![]() ·BP·AP=3,
·BP·AP=3,
∴BP·AP=6,
∵P是AC的中點,
∴A點的縱坐標是B點縱坐標的2倍,
又∵點A、B都在雙曲線![]()
![]() 上,
上,
∴B點的橫坐標是A點橫坐標的2倍,
∴OC=DP=BP,
∴|k| =OC·AC=BP·2AP=12.
又∵該函數圖像在第二象限
∴k=-12
∴該雙曲線的解析式是:![]() .
.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系內,己知![]() ,直線
,直線![]() 過
過![]() ,
,![]() 、
、![]() 關于
關于![]() 的對稱點分別為
的對稱點分別為![]() ,請利用直尺(無刻度)和圓規按下列要求作圖.
,請利用直尺(無刻度)和圓規按下列要求作圖.
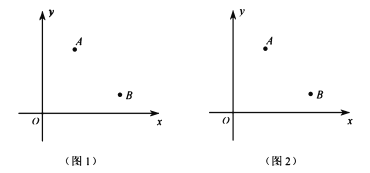
(l)當![]() 與
與![]() 重合時,請在圖
重合時,請在圖![]() 中畫出點
中畫出點![]() 位置,并求出
位置,并求出![]() 的值;
的值;
(2)當![]() 都落在
都落在![]() 軸上時,請在圖2中畫出直線
軸上時,請在圖2中畫出直線![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華傳統文化,某校開展“雙劇進課堂”的活動,該校童威隨機抽取部分學生,按四個類別:![]() 表示“很喜歡”,
表示“很喜歡”,![]() 表示“喜歡”,
表示“喜歡”,![]() 表示“一般”,
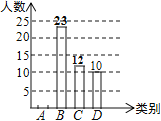
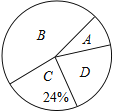
表示“一般”,![]() 表示“不喜歡”,調查他們對漢劇的喜愛情況,將結果繪制成如下兩幅不完整的統計圖,根據圖中提供的信息,解決下列問題:
表示“不喜歡”,調查他們對漢劇的喜愛情況,將結果繪制成如下兩幅不完整的統計圖,根據圖中提供的信息,解決下列問題:
(1)這次共抽取_________名學生進行統計調查,扇形統計圖中,![]() 類所對應的扇形圓心角的大小為__________
類所對應的扇形圓心角的大小為__________
(2)將條形統計圖補充完整
(3)該校共有1500名學生,估計該校表示“喜歡”的![]() 類的學生大約有多少人?
類的學生大約有多少人?
各類學生人數條形統計圖各類學生人數扇形統計圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點到直線的距離即為點到直線的垂線段的長.
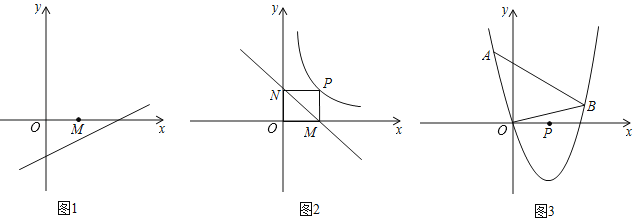
(1)如圖1,取點M(1,0),則點M到直線l:y=![]() x﹣1的距離為多少?
x﹣1的距離為多少?
(2)如圖2,點P是反比例函數y=![]() 在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=
在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=![]() ?若存在,求出點P的坐標,若不存在,請說明理由.
?若存在,求出點P的坐標,若不存在,請說明理由.
(3)如圖3,若直線y=kx+m與拋物線y=x2﹣4x相交于x軸上方兩點A、B(A在B的左邊).且∠AOB=90°,求點P(2,0)到直線y=kx+m的距離最大時,直線y=kx+m的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數![]() (a,b為常數,且
(a,b為常數,且![]() )與反比例函數
)與反比例函數![]() (m為常數,且
(m為常數,且![]() )的圖象交于點A(﹣2,1)、B(1,n).
)的圖象交于點A(﹣2,1)、B(1,n).

(1)求反比例函數和一次函數的解析式;
(2)連結OA、OB,求△AOB的面積;
(3)直接寫出當![]() 時,自變量x的取值范圍.
時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
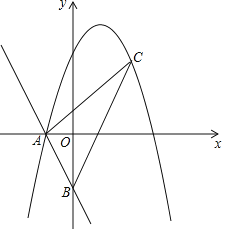
【題目】一次函數y=﹣2x﹣2分別與x軸、y軸交于點A、B.頂點為(1,4)的拋物線經過點A.
(1)求拋物線的解析式;
(2)點C為第一象限拋物線上一動點.設點C的橫坐標為m,△ABC的面積為S.當m為何值時,S的值最大,并求S的最大值;
(3)在(2)的結論下,若點M在y軸上,△ACM為直角三角形,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀下列材料,并完成相應的任務.
梅涅勞斯(Menelaus)是公元一世紀時的希臘數學家兼天文學家,著有幾何學和三角學方面的許多書籍.梅涅勞斯發現,三角形各邊(或其延長線)被一條不過任何一個頂點也不與任何一條邊平行的直線所截,這條直線可能與三角形的兩條邊相交(一定還會與一條邊的延長線相交),也可能與三條邊都不相交(與三條邊的延長線都相交).他進行了深入研究并證明了著名的梅涅勞斯定理(簡稱梅氏定理):
設D,E,F依次是△ABC的三邊AB,BC,CA或其延長線上的點,且這三點共線,則滿足![]() .
.
這個定理的證明步驟如下:
情況①:如圖1,直線DE交△ABC的邊AB于點D,交邊AC于點F,交邊BC的延長線與點E.
過點C作CM∥DE交AB于點M,則![]() ,
,![]() (依據),
(依據),
∴![]() =
=![]() ,
,
∴BEADFC=BDAFEC,即![]() .
.
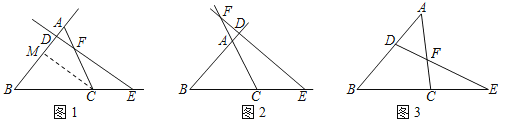
情況②:如圖2,直線DE分別交△ABC的邊BA,BC,CA的延長線于點D,E,F.
…
(1)情況①中的依據指: ;
(2)請你根據情況①的證明思路完成情況②的證明;
(3)如圖3,D,F分別是△ABC的邊AB,AC上的點,且AD:DB=CF:FA=2:3,連接DF并延長,交BC的延長線于點E,那么BE:CE= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形 ABCD 中,E 為邊 BC 上一點,F 為邊 CD 上一點,且∠AEF=90°.
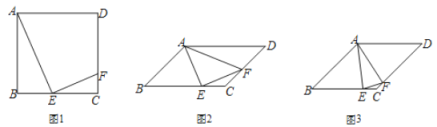
(1)如圖 1,若 ABCD 為正方形,E 為 BC 中點,求證:![]() .
.
(2)若 ABCD 為平行四邊形,∠AFE=∠ADC,
①如圖 2,若∠AFE=60°,求![]() 的值;
的值;
②如圖 3,若 AB=BC,EC=2CF.直接寫出 cos∠AFE 值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com