
【題目】(1)操作發現:
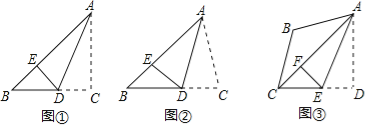
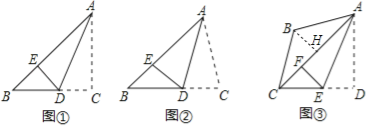
如圖①,在Rt△ABC中,∠C=2∠B=90°,點D是BC上一點,沿AD折疊△ADC,使得點C恰好落在AB上的點E處.請寫出AB、AC、CD之間的關系 ;
(2)問題解決:
如圖②,若(1)中∠C≠90°,其他條件不變,請猜想AB、AC、CD之間的關系,并證明你的結論;
(3)類比探究:
如圖③,在四邊形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=DC,連接AC,點E是CD上一點,沿AE折疊,使得點D正好落在AC上的F處,若BC=![]() ,直接寫出DE的長.
,直接寫出DE的長.
【答案】(1)AB=AC+CD;(2)AB=AC+CD;證明見試題解析;(3)DE的長為![]() .
.
【解析】
試題本題考查了折疊的性質:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.也考查了等腰三角形的性質和解直角三角形.(1)如圖①,設CD=t,由∠C=2∠B=90°易得△ABC為等腰直角三角形,則AC=BC,AB=![]() AC,再根據折疊的性質得DC=DE,∠AED=∠C=90°,又可判斷△BDE為等腰直角三角形,所以BD=
AC,再根據折疊的性質得DC=DE,∠AED=∠C=90°,又可判斷△BDE為等腰直角三角形,所以BD=![]() DE,則BD=
DE,則BD=![]() t,AC=BC=
t,AC=BC=![]() t+t=(
t+t=(![]() +1)t,AB=
+1)t,AB=![]() (
(![]() +1)t=t,從而得到AB=AC+CD;(2)如圖②,根據折疊的性質得DC=DE,∠AED=∠C,AE=AC,而∠C=2∠B,則∠AED=2∠B,根據三角形外角性質得∠AED=∠B+∠BDE,所以∠B=∠BDE,則EB=ED,所以ED=CD,于是得到AB=AE+BE=AC+CD;(3)作BH⊥AC于H,如圖③,設DE=x,利用(1)的結論得AC=x,根據等腰三角形的性質由BA=BC,∠CBA=120°得到∠BCA=∠BAC=30°,且CH=AH=
+1)t=t,從而得到AB=AC+CD;(2)如圖②,根據折疊的性質得DC=DE,∠AED=∠C,AE=AC,而∠C=2∠B,則∠AED=2∠B,根據三角形外角性質得∠AED=∠B+∠BDE,所以∠B=∠BDE,則EB=ED,所以ED=CD,于是得到AB=AE+BE=AC+CD;(3)作BH⊥AC于H,如圖③,設DE=x,利用(1)的結論得AC=x,根據等腰三角形的性質由BA=BC,∠CBA=120°得到∠BCA=∠BAC=30°,且CH=AH=![]() AC=
AC=![]() x,在Rt△BCH中,利用30度的余弦得cos30°=
x,在Rt△BCH中,利用30度的余弦得cos30°=![]() =
=![]() ,即
,即![]() x=
x=![]() ,然后解方程求出x即可.
,然后解方程求出x即可.
試題解析:(1)如圖①,設CD=t,∵∠C=2∠B=90°,∴∠B=45°,∠BAC=45°,∴△ABC為等腰直角三角形,∴AC=BC,AB=![]() AC,∵AD折疊△ADC,使得點C恰好落在AB上的點E處,∴DC=DE,∠AED=∠C=90°,
AC,∵AD折疊△ADC,使得點C恰好落在AB上的點E處,∴DC=DE,∠AED=∠C=90°,
∴△BDE為等腰直角三角形,∴BD=![]() DE,∴BD=
DE,∴BD=![]() t,∴AC=BC=
t,∴AC=BC=![]() t+t=(
t+t=(![]() +1)t,∴AB=
+1)t,∴AB=![]() (
(![]() +1)t=t,∴AB=AC+CD;
+1)t=t,∴AB=AC+CD;
(2)AB=AC+CD.理由如下:如圖②,∵AD折疊△ADC,使得點C恰好落在AB上的點E處,∴DC=DE,∠AED=∠C,AE=AC,∵∠C=2∠B,∴∠AED=2∠B,而∠AED=∠B+∠BDE,∴∠B=∠BDE,∴EB=ED,
∴ED=CD,∴AB=AE+BE=AC+CD;
(3)作BH⊥AC于H,如圖③,設DE=x,由(1)的結論得AC=x,∵BA=BC,∠CBA=120°,∴∠BCA=∠BAC=30°,∵BH⊥AC,∴CH=AH=![]() AC=
AC=![]() x,在Rt△BCH中,cos30°=
x,在Rt△BCH中,cos30°=![]() =
=![]() ,
,
∴![]() x=
x=![]() ,解得x=
,解得x=![]() ,即DE的長為
,即DE的長為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
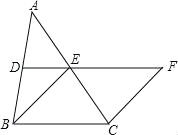
【題目】如圖,在△ABC中,D、E分別是AB、AC的中點,BE=2DE,延長DE到點F,使得EF=BE,連接CF.
(1)求證:四邊形BCFE是菱形;
(2)若CE=2,∠BCF=120°,求菱形BCFE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有長為24m的籬笆,一面利用墻(墻的最大可用長度a為10m),圍成中間隔有一道籬笆的長方形花圃.設花圃的寬AB為xm,面積為Sm2.

(1)求S與x的函數關系式;
(2)如果要圍成面積為45m2的花圃,AB的長是多少米?
(3)能圍成面積比45 m2更大的花圃嗎?如果能,請求出最大面積,并說明圍法;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實踐操作
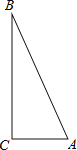
如圖,![]() 是直角三角形,
是直角三角形,![]() ,利用直尺和圓規按下列要求作圖,并在圖中表明相應的字母.(保留作圖痕跡,不寫作法)
,利用直尺和圓規按下列要求作圖,并在圖中表明相應的字母.(保留作圖痕跡,不寫作法)
(1)①作![]() 的平分線,交
的平分線,交![]() 于點
于點![]() ;②以
;②以![]() 為圓心,
為圓心,![]() 為半徑作圓.
為半徑作圓.
綜合運用
在你所作的圖中,
(2)![]() 與⊙
與⊙![]() 的位置關系是 ;(直接寫出答案)
的位置關系是 ;(直接寫出答案)
(3)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半徑.
的半徑.
(4)在(3)的條件下,求以![]() 為軸把△ABC旋轉一周得到的圓錐的側面積.
為軸把△ABC旋轉一周得到的圓錐的側面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,將△ABC繞頂點C逆時針旋轉得到△A′B′C,M是BC的中點,P是A′B′的中點,連接PM,若BC=2,∠BAC=30°,則線段PM的最大值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE = AF

(1)求證:BE = DF;
(2)連接AC交EF于點O,延長OC至點M,使OM = OA,連接EM、FM.判斷四邊形AEMF是什么特殊四邊形?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABD與△GDF都是等腰直角三角形,BD與DF均為斜邊(BD<DF).
(1)如圖1,B,D,F在同一直線上,過F作MF⊥GF于點F,取MF=AB,連結AM交BF于點H,連結GA,GM.
①求證:AH=HM;
②請判斷△GAM的形狀,并給予證明;
③請用等式表示線段AM,BD,DF的數量關系,并說明理由.
(2)如圖2,GD⊥BD,連結BF,取BF的中點H,連結AH并延長交DF于點M,請用等式直接寫出線段AM,BD,DF的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=ax2+c(a≠0)與x軸交于點A和點B(![]() ,0),與y軸交于點C(0,2),點P(2,t)是該拋物線上一點.
,0),與y軸交于點C(0,2),點P(2,t)是該拋物線上一點.

(1)求此拋物線的解析式及t的值;
(2)若點D是y軸上一點,線段PD繞點D逆時針旋轉90°后,點P的對應點P′恰好也落在此拋物線上,求點D的坐標;
(3)如圖2,直線l:y=kx+b交該拋物線于M、N兩點,且滿足MC⊥NC,設點P到直線l的距離是d,求d的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com