
【題目】如圖,在梯形ABCD中,AD//BC,E是BC的中點,AD=5,BC=12,CD=![]() ,∠C=45°,點P是BC邊上一動點,設PB的長為x。
,∠C=45°,點P是BC邊上一動點,設PB的長為x。
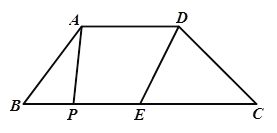
(1)梯形ABCD的面積為_________;
(2)當x的值為___________時,以點P、A、D、E為頂點的四邊形為直角梯形;
(3)當x的值為___________時,以點P、A、D、E為頂點的四邊形為平行四邊形;
(4)點P在BC邊上運動的過程中,以P、A、D、E為頂點的四邊形能否構成菱形?試說明理由。
【答案】(1)34
(2) x的值為3或8時,以點P、A、D、E為頂點的四邊形為直角梯形;
(3)x的值為1或11時,以點P、A、D、E為頂點的四邊形為平行四邊形;
(4)由(3)知,①當BP=1時,不能構成菱形.
②當BP′=11時,以點P、A、D、E為頂點的四邊形能構成菱形;
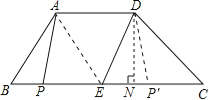
【解析】試題分析:(1)先作高,然后根據梯形的面積公式求出結果;
(2)如圖,分別過A、D作AM⊥BC于M,DN⊥CB于N,容易得到AM=DN,AD=MN,而CD=![]() ,∠C=45°,由此可以求出AM=DN,又AD=5,容易求出BM、CN,若點P、A、D、E為頂點的四邊形為直角梯形,則∠APC=90°或∠DPE=90°,那么P與M重合或E與N重合,即可求出此時的x的值;
,∠C=45°,由此可以求出AM=DN,又AD=5,容易求出BM、CN,若點P、A、D、E為頂點的四邊形為直角梯形,則∠APC=90°或∠DPE=90°,那么P與M重合或E與N重合,即可求出此時的x的值;
(3)若以點P、A、D、E為頂點的四邊形為平行四邊形,那么AD=PE,有兩種情況:①當P在E的左邊,利用已知條件可以求出BP的長度;②當P在E的右邊,利用已知條件也可求出BP的長度;
(4)以點P、A、D、E為頂點的四邊形能構成菱形.由(2)知,當BP=11時,以點P、A、D、E為頂點的四邊形是平行四邊形,根據已知條件分別計算一組鄰邊證明它們相等即可證明它是菱形.


 精英口算卡系列答案
精英口算卡系列答案科目:初中數學 來源: 題型:
【題目】甲校男生占全校總人數的50%,乙校女生占全校總人數的50%,則甲乙兩校女生人數相比( )
A.甲校多于乙校
B.甲校少于乙校
C.甲乙兩校一樣多
D.不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
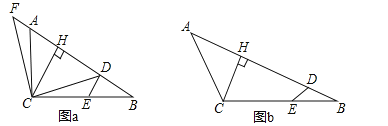
【題目】如圖,在△ABC中,BC>AC,點E在BC上,CE=CA,點D在AB上,連接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足為H.
(1)如圖a,當∠ACB=90°時,連接CD,過點C作CF⊥CD交BA的延長線于點F.
①求證:FA=DE;
②請猜想三條線段DE,AD,CH之間的數量關系,直接寫出結論;
(2)如圖b,當∠ACB=120°時,三條線段DE,AD,CH之間存在怎樣的數量關系?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元二次方程x2-(k+1)x=0有兩個不相等的實數根,則k的取值范圍為( )
A. k>-1 B. k<-1 C. k≠-1 D. k為任意實數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上兩點A、B,點A在點B的左邊,點A表示的數為a,點B表示的數為b,且A、B兩點的距離是8.
(1)點A與點B之間(包括A、B兩點)的整數有__________個;
(2)當a=-3時,b=_______;
(3)當![]() =5時,a=__________;
=5時,a=__________;
(4)當a取何值時, ![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(5)若![]() ,求a的范圍.
,求a的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“唱紅歌”比賽活動,九年級(1)、(2)班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績如圖所示.
班級 | 平均數(分) | 中位數 | 眾數 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根據圖示填寫上表;
(2)結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
(3)計算兩班復賽成績的方差,并說明哪個班級的成績較穩定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com