
【題目】如圖,⊙O是△ABC的外接圓,AB為直徑,D是⊙O上一點,且弧CB=弧CD,CE⊥DA交DA的延長線于點E.
(1)求證:∠CAB=∠CAE;
(2)求證:CE是⊙O的切線;
(3)若AE=1,BD=4,求⊙O的半徑長.

【答案】(1)見解析;(2)見解析;(3)![]() .
.
【解析】
(1)連接BD,根據圓內接四邊形的性質和等弧所對的圓周角相等,可得∠CAB=∠CAE;
(2)連接OC,由題意可得∠ACB=90°=∠AEC,即可證∠BCO=∠ACE=∠ABC,可得∠ECO=∠ACB=90°,則可證CE是⊙O的切線;
(3)過點C作CF⊥AB于點F,由角平分線的性質可得CE=CF,可證△CED≌△CFB,可得DE=BF,根據勾股定理可求⊙O的半徑長.
證明:(1)連接BD
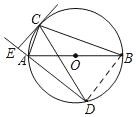
∵弧CB=弧CD,
∴∠CDB=∠CBD,CD=BC
∵四邊形ACBD是圓內接四邊形
∴∠CAE=∠CBD,且∠CAB=∠CDB,
∴∠CAB=∠CAE;
(2)連接OC
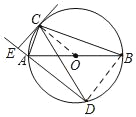
∵AB為直徑,
∴∠ACB=90°=∠AEC,
又∵∠CAB=∠CAE,
∴∠ABC=∠ACE,
∵OB=OC,
∴∠BCO=∠CBO,
∴∠BCO=∠ACE,
∴∠ECO=∠ACE+∠ACO=∠BCO+∠ACO=∠ACB=90°,
∴EC⊥OC,
∵OC是⊙O的半徑,
∴CE是⊙O的切線.
(3)過點C作CF⊥AB于點F,
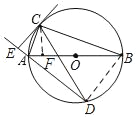
又∵∠CAB=∠CAE,CE⊥DA,
∴AE=AF,
在△CED和△CFB中,
∵∠DEC=∠BFC=90°,
∠EDC=∠BFC,
CD=BC,
∴△CED≌△CFB(AAS),
∴ED=FB,
設AB=x,則AD=x﹣2,
在△ABD中,由勾股定理得,x2=(x﹣2)2+42,
解得,x=5,
∴⊙O的半徑的長為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
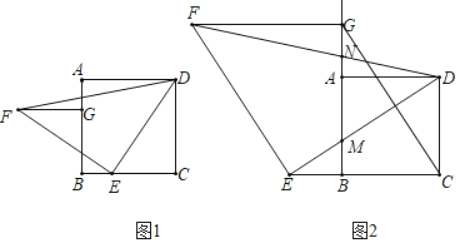
【題目】如圖1,在正方形ABCD中,E是邊BC上的點,將線段DE繞點E逆時針旋轉90°得到EF,過點C作CG∥EF交BA(或其延長線)于點G,連接DF,FG.
(1)FG與CE的數量關系是 ,位置關系是 .
(2)如圖2,若點E是CB延長線上的點,其它條件不變.
①(1)中的結論是否仍然成立?請作出判斷,并給予證明;
②DE,DF分別交BG于點M,N,若BC=2BE,求![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
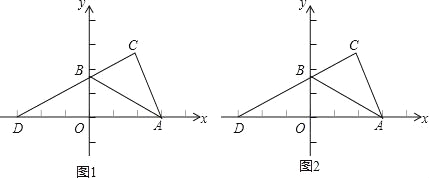
【題目】如圖,Rt△AOB在平面直角坐標系中,已知:B(0,![]() ),點A在x軸的正半軸上,OA=3,∠BAD=30°,將△AOB沿AB翻折,點O到點C的位置,連接CB并延長交x軸于點D.
),點A在x軸的正半軸上,OA=3,∠BAD=30°,將△AOB沿AB翻折,點O到點C的位置,連接CB并延長交x軸于點D.
(1)求點D的坐標;
(2)動點P從點D出發,以每秒2個單位的速度沿x軸的正方向運動,當△PAB為直角三角形時,求t的值;
(3)在(2)的條件下,當△PAB為以∠PBA為直角的直角三角形時,在y軸上是否存在一點Q使△PBQ為等腰三角形?如果存在,請直接寫出Q點的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了預防“甲型H1N1”,某校對教室采用藥薰消毒法進行消毒,已知藥物燃燒時,室內每立方米空氣中的含藥量y(mg)與時間x(min)成正比例,藥物燃燒后,y與x成反比例,如圖所示,現測得藥物8min燃畢,此時室內空氣每立方米的含藥量為6mg,請你根據題中提供的信息,解答下列問題:
(1)藥物燃燒時,求y關于x的函數關系式?自變量x的取值范圍是什么?藥物燃燒后y與x的函數關系式呢?
(2)研究表明,當空氣中每立方米的含藥量低于1.6mg時,生方可進教室,那么從消毒開始,至少需要幾分鐘后,生才能進入教室?
(3)研究表明,當空氣中每立方米的含藥量不低于3mg且持續時間不低于10min時,才能殺滅空氣中的毒,那么這次消毒是否有效?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
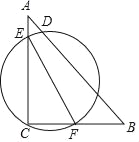
【題目】如圖,△ABC中,∠C=90°,AC=8,BC=6,E,F分別在邊AC,BC,若以EF為直徑作圓經過AB上某點D,則EF長的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
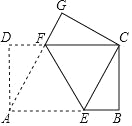
【題目】如圖,四邊形ABCD為矩形,點E在AB上,點F在CD上,以EF為折痕,將此矩形折疊,使點A和點C重合,點D和點G重合.
(1)求證:四邊形AECF是菱形.
(2)若AB=5,AD=3,則菱形AECF的面積等于_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
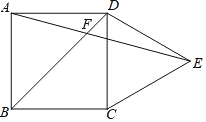
【題目】如圖,正方形ABCD,將邊CD繞點C順時針旋轉60°,得到線段CE,連接DE,AE,BD交于點F.
(1)求∠AFB的度數;
(2)求證:BF=EF;
(3)連接CF,直接用等式表示線段AB,CF,EF的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,以AC為直徑作⊙O,交AB于D,過點O作OE∥AB,交BC于E.
(1)求證:ED為⊙O的切線;
(2)如果⊙O的半徑為![]() ,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.
,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.

【答案】(1)證明見解析;(2)![]()
【解析】試題分析:(1)首先連接OD,由OE∥AB,根據平行線與等腰三角形的性質,易證得![]() ≌
≌![]() 即可得
即可得![]() ,則可證得
,則可證得![]() 為
為![]() 的切線;
的切線;
(2)連接CD,根據直徑所對的圓周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的長,又由OE∥AB,證得
的長,又由OE∥AB,證得![]() 根據相似三角形的對應邊成比例,即可求得
根據相似三角形的對應邊成比例,即可求得![]() 的長,然后利用三角函數的知識,求得
的長,然后利用三角函數的知識,求得![]() 與
與![]() 的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
試題解析:(1)證明:連接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切線;
的切線;
(2)連接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直徑,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面積為![]()

【題型】解答題
【結束】
25
【題目】【題目】已知,拋物線y=ax2+ax+b(a≠0)與直線y=2x+m有一個公共點M(1,0),且a<b.
(1)求b與a的關系式和拋物線的頂點D坐標(用a的代數式表示);
(2)直線與拋物線的另外一個交點記為N,求△DMN的面積與a的關系式;
(3)a=﹣1時,直線y=﹣2x與拋物線在第二象限交于點G,點G、H關于原點對稱,現將線段GH沿y軸向上平移t個單位(t>0),若線段GH與拋物線有兩個不同的公共點,試求t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
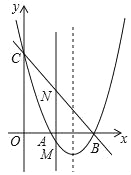
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A和B(3,0),與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)若點M是拋物線上在x軸下方的動點,過M作MN∥y軸交直線BC于點N,求線段MN的最大值;
(3)E是拋物線對稱軸上一點,F是拋物線上一點,是否存在以A,B,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com