
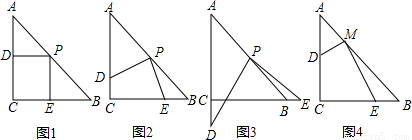
 ∠ACB=45°.
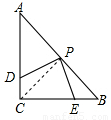
∠ACB=45°. ,此時PB=BE;
,此時PB=BE;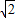 時,此時PB=EB;
時,此時PB=EB;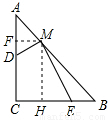
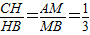 ,HB=MH,
,HB=MH,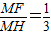 .
.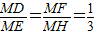 .
.

 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源:2005年全國中考數學試題匯編《圖形的相似》(07)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2005年全國中考數學試題匯編《圖形的旋轉》(03)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2005年全國中考數學試題匯編《四邊形》(10)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2005年山東省青島市中考數學試卷(課標卷)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com