
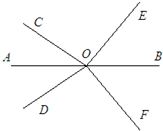
 (x>0)的圖象交于點C(2,n).
(x>0)的圖象交于點C(2,n). (x>0)相交于點M、N,若MN=5PM,求直線PQ的解析式.
(x>0)相交于點M、N,若MN=5PM,求直線PQ的解析式.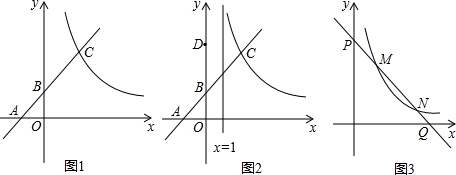
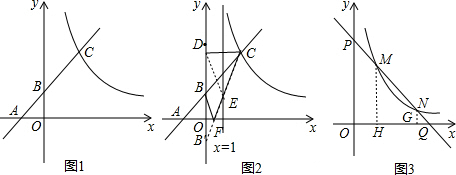
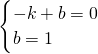 ,解得
,解得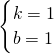 ,
, 得k=2×3=6,
得k=2×3=6, ;
;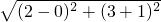 =2+2
=2+2 ;
;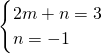 ,解得
,解得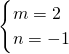 ,
, ,
, ,0);
,0);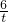 ),則N(6t,
),則N(6t, ),
),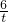 ),N(6t,
),N(6t, )在直線PQ上,
)在直線PQ上,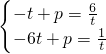 ,解得
,解得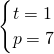 或
或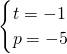 (舍去),
(舍去), ,從而得到最小周長=2+2
,從而得到最小周長=2+2 ;再待定系數法求出直線CB′的解析式為y=2x-1,則把x=1或y=0分別代入y=2x-1可得到E點和F點坐標;
;再待定系數法求出直線CB′的解析式為y=2x-1,則把x=1或y=0分別代入y=2x-1可得到E點和F點坐標; ),則N(6t,
),則N(6t, ),設直線PQ的解析式為y=-x+p,然后M點、N點坐標代入得到關于t與p的方程組,再解方程組即可.
),設直線PQ的解析式為y=-x+p,然后M點、N點坐標代入得到關于t與p的方程組,再解方程組即可.

 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
 21、如圖,若直線AB分別平分∠COD和∠EOF.
21、如圖,若直線AB分別平分∠COD和∠EOF.查看答案和解析>>
科目:初中數學 來源: 題型:
| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
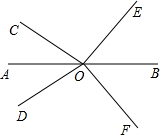 如圖,若直線AB分別平分∠COD和∠EOF.
如圖,若直線AB分別平分∠COD和∠EOF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,若直線AB分別平分∠COD和∠EOF.
如圖,若直線AB分別平分∠COD和∠EOF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com