
【題目】某高中學校為使高一新生入校后及時穿上合身的校服,現提前對某校九年級(1)班學生即將所穿校服型號情況進行摸底調查,并根據調查結果繪制如圖兩個不完整的統計圖(校服型號以身高作為標準,共分為6種型號).
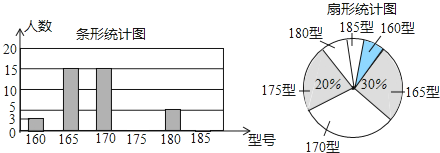
根據以上信息,解答下列問題:
(1)該班共有多少名學生?
(2)在條形統計圖中,請把空缺部分補充完整;在扇形統計圖中,請計算185型校服所對應的扇形圓心角的大小;
(3)求該班學生所穿校服型號的眾數和中位數.如果該高中學校準備招收2000名高一新生,則估計需要準備多少套180型號的校服?
【答案】(1)共有50名學生;(2)答案見解析;14.4°;(3)眾數是165和170;中位數是170,200套.
【解析】
(1)利用總人數=165型的人數÷對應的百分比求解即可;
(2)先求出175,185型的學生人數,再補全統計圖即可,
(3)利用眾數,中位數的定義及2000乘180型號所占的百分比求解即可.
解:(1)15÷30%=50(名),50×20%=10(名),
答:該班共有50名學生,其中穿175型校服的學生有10名;
(2)穿175型校服的學生有10名:50×20%=10(名),
185型的學生人數為:50-3-15-15-10-5=50-48=2(名),
補全統計圖如圖所示;
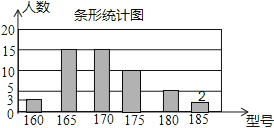
185型校服所對應的扇形圓心角為:![]() ×360°=14.4°;
×360°=14.4°;
(3)165型,170型學生最多,均為15人
∴該班學生所穿校服型號的眾數為165,170,
將型號從小到大排列后,第25名和第26名同學均為170型
∴中位數為170.
2000![]() (套)
(套)
∴需要準備200套180型號的校服.


科目:初中數學 來源: 題型:
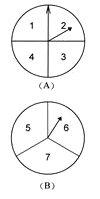
【題目】甲乙兩人在玩轉盤游戲時,把轉盤A、B分別分成4等份、3等份,并在每一份內標上數字,如圖所示.游戲規定,轉動兩個轉盤停止后,指針所指的兩個數字之和為奇數時,甲獲勝;為偶數時,乙獲勝.
(1)用列表法(或畫樹狀圖)求甲獲勝的概率;
(2)你認為這個游戲規則對雙方公平嗎?請簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學組織七、八、九年級學生參加“州慶60年,夢想紅河”作文比賽.該校將收到的參賽作文進行分年級統計,繪制了如圖1和圖2兩幅不完整的統計圖. 根據圖中提供的信息完成以下問題.
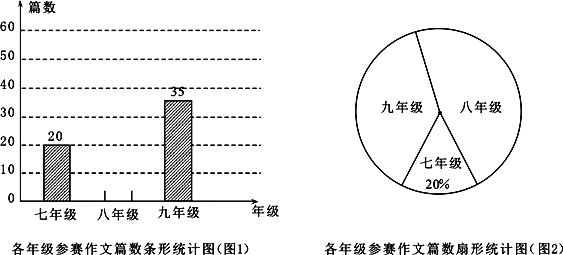
(1)扇形統計圖中九年級參賽作文篇數對應的圓心角是 度,并補全條形統計圖;
(2)經過評審,全校有4篇作文榮獲特等獎,其中有一篇來自七年級,學校準備從特等獎作文中任選兩篇刊登在校刊上,把七年級特等獎作文被選登在校刊上的事件記為A,其它年級特等獎作文被選登在校刊上的事件分別記為B,C,D. 請利用畫樹狀圖或列表的方法求出七年級特等獎作文被選登在校刊上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
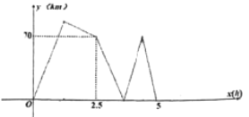
【題目】甲乙兩地相距300![]() ,一輛貨車和一輛轎車先后從甲地出發到乙地停止,貨車先出發從甲地勻速開往乙地,貨車開出一段時間后,轎車出發,勻速行駛一段時間后接到通知提速后勻速趕往乙地(提速時間不計),最后發現轎車比貨車提前0.5小時到達,下圖表示兩車之間的距離
,一輛貨車和一輛轎車先后從甲地出發到乙地停止,貨車先出發從甲地勻速開往乙地,貨車開出一段時間后,轎車出發,勻速行駛一段時間后接到通知提速后勻速趕往乙地(提速時間不計),最后發現轎車比貨車提前0.5小時到達,下圖表示兩車之間的距離![]() 與貨車行駛的時間
與貨車行駛的時間![]() 之間的關系,則貨車行駛__________小時.兩車在途中相遇.
之間的關系,則貨車行駛__________小時.兩車在途中相遇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,拋物線的頂點記為
兩點,拋物線的頂點記為![]() .其對稱軸與
.其對稱軸與![]() 軸的交點記為
軸的交點記為![]() ;
;
(1)如圖1,在線段![]() 上有兩個動點
上有兩個動點![]() 、
、![]() ,且
,且![]() ,作
,作![]() 軸,分別交拋物線于點
軸,分別交拋物線于點![]() 、
、![]() ,過點
,過點![]() 作另一條直線
作另一條直線![]() ,當
,當![]() 取得最大值時,有一動點
取得最大值時,有一動點![]() 從
從![]() 出發沿某條路徑以1個單位每秒的速度先運動到直線
出發沿某條路徑以1個單位每秒的速度先運動到直線![]() 上的點
上的點![]() 處,再沿垂直于
處,再沿垂直于![]() 的方向以1個單位每秒的速度從點
的方向以1個單位每秒的速度從點![]() 運動到
運動到![]() 上
上![]() 點處,最后以
點處,最后以![]() 個單位每秒的速度從點
個單位每秒的速度從點![]() 回到點
回到點![]() ,運動停止,請求出滿足條件的
,運動停止,請求出滿足條件的![]() 點坐標及動點
點坐標及動點![]() 運動總時間的最小值;
運動總時間的最小值;
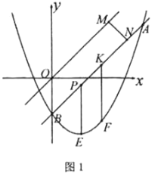
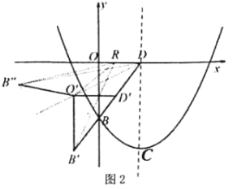
(2)如圖2,連接![]() ,將
,將![]() 沿射線
沿射線![]() 平移得
平移得![]() ,當
,當![]() 恰好落在∠BDO的角平分線上時,在
恰好落在∠BDO的角平分線上時,在![]() 軸上取一點
軸上取一點![]() ,再將
,再將![]() 沿
沿![]() 翻折得
翻折得![]() ,連接
,連接![]() 、
、![]() ,當
,當![]() 為等腰三角形時,求出
為等腰三角形時,求出![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
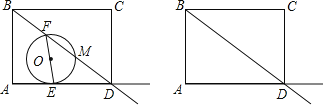
【題目】如圖,矩形ABCD中,AB=6,AD=8.動點E,F同時分別從點A,B出發,分別沿著射線AD和射線BD的方向均以每秒1個單位的速度運動,連接EF,以EF為直徑作⊙O交射線BD于點M,設運動的時間為t.
(1)當點E在線段AD上時,用關于t的代數式表示DE,DM.
(2)在整個運動過程中,
①連結CM,當t為何值時,△CDM為等腰三角形.
②圓心O處在矩形ABCD內(包括邊界)時,求t的取值范圍,并直接寫出在此范圍內圓心運動的路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
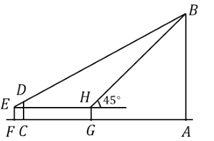
【題目】小明準備利用所學的知識測量旗桿![]() 的高度.他設計了如下的測量方案:選取一個合適觀測點,在地面
的高度.他設計了如下的測量方案:選取一個合適觀測點,在地面![]() 處垂直地面豎立高度為2米的標桿
處垂直地面豎立高度為2米的標桿![]() ,小明調整自己的位置到
,小明調整自己的位置到![]() 處,使得視線與
處,使得視線與![]() 、
、![]() 在同一直線上,此時測得
在同一直線上,此時測得![]() 米,然后小明沿著
米,然后小明沿著![]() 方向前進11米到
方向前進11米到![]() 處,利用隨身攜帶的等腰直角三角形測得
處,利用隨身攜帶的等腰直角三角形測得![]() 點的仰角為45°,已知小明眼睛到地面距離為1.5米(
點的仰角為45°,已知小明眼睛到地面距離為1.5米(![]() 米),請你根據題中所給的數據計算旗桿的高度.
米),請你根據題中所給的數據計算旗桿的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.

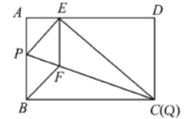
圖1 圖2
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() ,
,![]() 也隨之移動;
也隨之移動;
①當點![]() 與點
與點![]() 重合時(如圖2),求菱形
重合時(如圖2),求菱形![]() 的邊長;
的邊長;
②若限定![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上移動,則點
上移動,則點![]() 在邊
在邊![]() 上移動的最大距離是_______.
上移動的最大距離是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“奔跑吧,兄弟!”節目組,預設計一個新的游戲:“奔跑”路線需經A、B、C、D四地.如圖,其中A、B、C三地在同一直線上,D地在A地北偏東30°方向、在C地北偏西45°方向.C地在A地北偏東75°方向.且BD=BC=30m.從A地到D地的距離是( )

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com