
【題目】如圖,等邊三角形![]() 的邊長為4厘米,長為1厘米的線段
的邊長為4厘米,長為1厘米的線段![]() 在
在![]() 的邊
的邊![]() 上沿
上沿![]() 方向以1厘米/秒的速度向點
方向以1厘米/秒的速度向點![]() 運動(運動開始時,點
運動(運動開始時,點![]() 與點
與點![]() 重合,點
重合,點![]() 到達點
到達點![]() 時運動終止),過點
時運動終止),過點![]() 、
、![]() 分別作
分別作![]() 邊的垂線,與
邊的垂線,與![]() 的其他邊交于
的其他邊交于![]() 、
、![]() 兩點.線段
兩點.線段![]() 在運動的過程中,點
在運動的過程中,點![]() 、
、![]() 、
、![]() 、
、![]() 圍成的圖形的面積為
圍成的圖形的面積為![]() 平方厘米,運動的時間為
平方厘米,運動的時間為![]() 秒.則大致反映
秒.則大致反映![]() 與
與![]() 變化關系的圖像是( )
變化關系的圖像是( )

A.  .
. 
C. 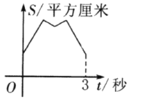 D.
D. 
【答案】A
【解析】
利用直角梯形的面積公式,由MN=1不變,可知四邊形MNQP的面積隨(PM+QN)的變化而變化,找到特殊點過點C作CG⊥AB,可分析得出四邊形MNQP的面積變化情況.
解:過點C作CG⊥AB,
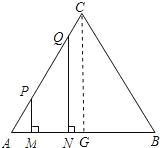
∵MN=1,四邊形MNQP為直角梯形,
∴四邊形MNQP的面積為S=![]() MN×(PM+QN),
MN×(PM+QN),
∴N點從A到G點四邊形MNQP的面積為S=![]() MN×(PM+QN)中,PM,QN都在增大,所以面積也增大;
MN×(PM+QN)中,PM,QN都在增大,所以面積也增大;
當QN=CG時,QN開始減小,但PM仍然增大,且PM+QN不變,
∴四邊形MNQP的面積不發生變化,
當PM<CG時,PM+QN開始減小,
∴四邊形MNQP的面積減小,
∴符合要求的只有A.
故選:A.


科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
在學習“可化為一元一次方程的分式方程及其解法”的過程中,老師提出一個問題:若關于x的分式方程![]() =1的解為正數,求a的取值范圍.
=1的解為正數,求a的取值范圍.
經過獨立思考與分析后,小杰和小哲開始交流解題思路如下:
小杰說:解這個關于x的分式方程,得x=a+4.由題意可得a+4>0,所以a>﹣4,問題解決.
小哲說:你考慮的不全面,還必須保證x≠4,即a+4≠4才行.
(1)請回答: 的說法是正確的,并簡述正確的理由是 ;
(2)參考對上述問題的討論,解決下面的問題:
若關于x的方程![]() 的解為非負數,求m的取值范圍.
的解為非負數,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農莊計劃在30畝空地上全部種植蔬菜和水果,菜農小張和果農小李分別承包了種植蔬菜和水果的任務.小張種植每畝蔬菜的工資y(元)與種植面積m(畝)之間的函數如圖①所示,小李種植水果所得報酬z(元)與種植面積n(畝)之間函數關系如圖②所示. 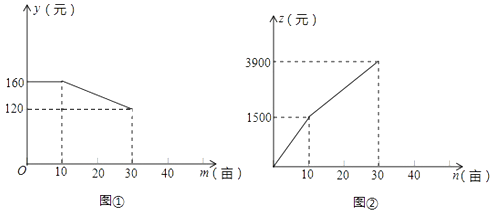
(1)如果種植蔬菜20畝,則小張種植每畝蔬菜的工資是元,小張應得的工資總額是元,此時,小李種植水果畝,小李應得的報酬是元;
(2)當10<n≤30時,求z與n之間的函數關系式;
(3)設農莊支付給小張和小李的總費用為w(元),當10<m≤30時,求w與m之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A是第一象限內橫坐標為2 ![]() 的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是 .
的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是 . 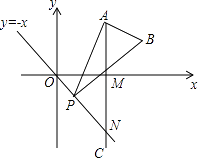
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,AB=2BC,現給出下列結論:①sinA= ![]() ;②cosB=
;②cosB= ![]() ;③tanA=
;③tanA= ![]() ;④tanB=
;④tanB= ![]() ,其中正確的結論是(只需填上正確結論的序號)
,其中正確的結論是(只需填上正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某公司有三個住宅區可看作一點,A,B,C各區分別住有職工30人、15人、10人,且這三個住宅區在一條大道上(A,B,C三點共線),已知AB=100米,BC=200米.為了方便職工上下班,該公司的接送車打算在此間只設一個停靠點,為使所有的人步行到停靠點的路程之和最小,那么該停靠點的位置應設在( )
![]()
A. 點A B. 點B
C. A,B之間 D. B,C之間
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平安加氣站某日8:00的儲氣量為10 000立方米.從8:00開始,3把加氣槍同時以每車20立方米的加氣量,依次給在加氣站排隊等候的若干輛車加氣.8:30時,為緩解排隊壓力,又增開了2把加氣槍.假設加氣過程中每把加氣槍加氣的速度是勻速的,在不關閉加氣槍的情況下,加氣站的儲氣量![]() (立方米)與時間
(立方米)與時間![]() (小時)之間的函數關系如圖中的折線
(小時)之間的函數關系如圖中的折線![]() 所示.
所示.
(1)分別求出8:00 ~8:30及8:30之后加氣站的儲氣量![]() (立方米)與時間
(立方米)與時間![]() (小時)之間的函數表達式.
(小時)之間的函數表達式.
(2)前30輛車能否在當天8:42之前加完氣?
(3)若前![]() 輛車按上述方式加氣,它們加完氣的時間要比不增開加氣槍加完氣的時間提前1個小時,求
輛車按上述方式加氣,它們加完氣的時間要比不增開加氣槍加完氣的時間提前1個小時,求![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com