【題目】二次函數y＝ax2+bx+c（a≠0），經過點（1.0），對稱軸l如圖所示，若M＝a+b﹣c，N＝2a﹣b，P＝a+c，則M，N，P中，值小于0的數有（ ）個．
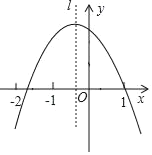
A.2B.1C.0D.3
【答案】A
【解析】
由二次函數y=ax2+bx+c（a≠0），經過點（1.0），和與y軸交點的位置，可以判斷M的符號；由拋物線的開口方向和對稱軸，可以判斷N的符號；由拋物線的開口、對稱軸的位置、和過（1，0）點可以判斷P的符號，最后綜合得出結論，做出選擇．
解：（1）∵二次函數y＝ax2+bx+c（a≠0），經過點（1.0），
∴a+b+c＝0，
又∵拋物線與y軸交在y軸的正半軸，
∴c＞0
∴a+b﹣c＜0，故M＜0；
（2）拋物線開口向下，因此a＜0，對稱軸在y軸左側，﹣1的右側，
∴﹣
＞﹣1，
∴2a﹣b＜0，故N＜0；
（3）拋物線開口向下，因此a＜0，對稱軸在y軸左側，因此a、b同號，∴b＜0
∵a+b+c＝0，
∴a+c=-b＞0，因此P＞0
綜上所述：M＜0，N＜0，P＞0；
故選A．
口算題卡北京婦女兒童出版社系列答案科目：初中數學 來源： 題型：
【題目】隨著信息技術的迅猛發展，人們去商場購物的支付方式更加多樣、便捷．某校數學興趣小組設計了一份調查問卷，要求每人選且只選一種你最喜歡的支付方式．現將調查結果進行統計并繪制成如下兩幅不完整的統計圖，請結合圖中所給的信息解答下列問題：
（1）這次活動共調查了 人；在扇形統計圖中，表示“支付寶”支付的扇形圓心角的度數為 ；
（2）將條形統計圖補充完整．觀察此圖，支付方式的“眾數”是“ ”；
（3）在一次購物中，小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付，請用畫樹狀圖或列表格的方法，求出兩人恰好選擇同一種支付方式的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1所示，在四邊形ABCD中，AD∥BC， AB⊥BC，∠DCB=75，以CD為一邊的等邊△DCE的另一頂點E在邊AB上．
(1)求∠AED的度數；
(2)連接AC，如圖2所示，試判斷△ABC的形狀；
(3)如圖3所示，若F為線段CD上一點，AB=4，∠FBC=30，求DF的長．
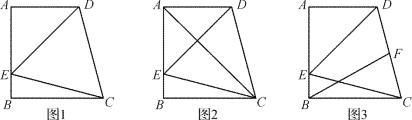
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為調查“停課不停學”期間九年級學生平均每天上網課時長，隨機抽取了
名九年級學生做網絡問卷調查．共四個選項：
小時以下)、
小時)、
小時)， 
小時以上)，每人只能選一
項．并將調查結果繪制成如下不完整的統計表和統計圖．
被調查學生平均每天上網課時間統計表
時長 | 所占百分比 |
|
|
|
|
|
|
|
|
合計 |
|
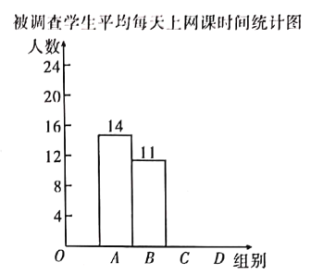
根據以上信息，解答下列問題：
，
，
補全條形統計圖；
該校有九年級學生
名，請你估計仝校九年級學生平均每天上網課時長在
小時及以上的共多少名；
在被調查的對象中，平均每天觀看時長超過
小時的，有
名來自九
班，
名來自九
班，其余都來自九
班，現教導處準備從
選項中任選兩名學生進行電話訪談，請用列表法或畫樹狀圖的方法求所抽取的名學生恰好來自同一個班級的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有A，B兩種商品，已知買一件A商品比買一件B商品少30元，用160元全部購買A商品的數量與用400元全部購買B商品的數量相同．
（1）A，B兩種商品每件各是多少元？
（2）如果小亮準備購買A，B兩種商品共10件，總費用不超過380元，且不低于300元，那么一共有幾種購買方案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“2018西安國際馬拉松”于2018年10月20日在陜西西安舉行，該賽事共有三項：
．“馬拉松”、
．“半程馬拉松”、
．“迷你馬拉松”小明和小剛有幸參與了該項賽事的志愿者服務工作，組委會隨機將志愿者分配到三個項目組．
（1）小明被分配到“迷你馬拉松”項目組的概率為________．
（2）利用列表或樹狀圖求小明和小剛被分配到不同項目組的概率________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，AB=4，E是BC邊的中點， F是CD邊上的一點， 且DF=1．若M、N分別是線段AD、AE上的動點，則MN+MF的最小值為________．
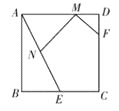
查看答案和解析>>
科目：初中數學 來源： 題型：
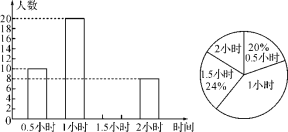
【題目】為增強學生的身體素質，教育行政部門規定學生每天參加戶外活動的平均時間不少于1小時．為了解學生參加戶外活動的情況，對部分學生參加戶外活動的時間進行了抽樣調查，并將調查結果繪制成如下兩幅不完整的統計圖，請你根據圖中提供的信息解答下列問題：
(1)在這次調查中共調查了多少名學生？
(2)求戶外活動時間為1.5小時的人數，并補全頻數分布直方圖；
(3)本次調查中學生參加戶外活動的平均時間是否符合要求？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，拋物線
與
軸交于B、C兩點（點B在點C右側），與
軸交于點
，連接
，
．
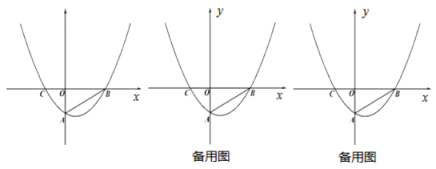
（1）求拋物線的解析式；
（2）點P在第二象限的拋物線上，連接PB交軸于D，取PB的中點E，過點E作
軸于點H，連接DH，設點P的橫坐標為
.
的面積為
，求與的函數關系式（不要求寫出自變量的取值范圍）；
（3）在（2）的條件下，作
軸于F，連接CP、CD，
，點為
上一點，連接
交軸于點
，連接BF并延長交拋物線于點
.
，在射線CS上取點Q.連接QF，
，求直線
的解析式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
