
【題目】正方形 ABCD 中,AB=3cm,動點 M 自A 點出發沿 AB 方向以每秒 1cm 的速度運動,同時點 N 自D 點出發沿折線 DC→CB 以每秒 2cm 的速度運動,到達 B 點時運動同時停止,設△AMN 的面積為 y(cm2),運動時間為 x(秒),則下列圖象中能大致反映 y 與 x 之間函數關系的是( )

A.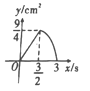 B.
B.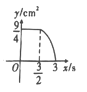 C.
C.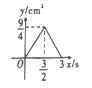 D.
D.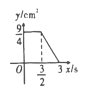
【答案】A
【解析】
分兩部分計算y的關系式:①當點N在CD上時,易得S△AMN的關系式,S△AMN的面積關系式為一個一次函數;②當點N在CB上時,底邊AM不變,表示出S△AMN的關系式,S△AMN的面積關系式為一個開口向下的二次函數.
∵點N自D點出發沿折線DCCB以每秒2cm的速度運動,到達B點時運動同時停止,
∴N到C的時間為:t=3÷2=1.5,
分兩部分:
①當0x1.5時,如圖1,此時N在DC上,
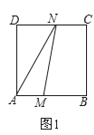
S△AMN=y=![]() AM×AD=
AM×AD=![]() x×3=
x×3=![]() x,S△AMN的面積關系式為一個一次函數
x,S△AMN的面積關系式為一個一次函數
②當1.5<x3時,如圖2,此時N在BC上,
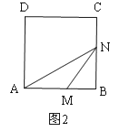
∴DC+CN=2x,
∴BN=62x,
∴S△AMN=y=![]() AM×BN=
AM×BN=![]() x(62x)=x2+3x,S△AMN的面積關系式為一個開口向下的二次函數.
x(62x)=x2+3x,S△AMN的面積關系式為一個開口向下的二次函數.
故選A.


科目:初中數學 來源: 題型:
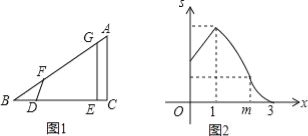
【題目】如圖1,△ABC中,∠C=90°,線段DE在射線BC上,且DE=AC,線段DE沿射線BC運動,開始時,點D與點B重合,點D到達點C時運動停止,過點D作DF=DB,與射線BA相交于點F,過點E作BC的垂線,與射線BA相交于點G.設BD=x,四邊形DEGF與△ABC重疊部分的面積為S,S關于x的函數圖象如圖2所示(其中0<x≤m,1<x≤m,m<x≤3時,函數的解析式不同)
(1)填空:BC的長是 ;
(2)求S關于x的函數關系式,并寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,∠ABC=90°,AB=BC=8cm,動點P從點A出發,以2cm/s的速度沿射線AB運動,同時動點Q從點C出發,以2cm/s的速度沿邊BC的延長線運動,PQ與直線AC相交于點D.設P點運動時間為t秒,△PCQ的面積為S cm2.
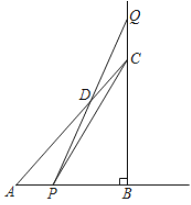
(1)直接寫出AC的長:AC= cm;
(2)求出S關于t的函數關系式,并求出當點P運動幾秒時,S△PCQ=S△ABC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦期間,某超市銷售兩種不同品牌的蘋果,已知1千克甲種蘋果和1千克乙種蘋果的進價之和為18元.當銷售1千克甲種蘋果和1千克乙種蘋果利潤分別為4元和2元時,陳老師購買3千克甲種蘋果和4千克乙種蘋果共用82元.
(1)求甲、乙兩種蘋果的進價分別是每千克多少元?
(2)在(1)的情況下,超市平均每天可售出甲種蘋果100千克和乙種蘋果140千克,若將這兩種蘋果的售價各提高1元,則超市每天這兩種蘋果均少售出10千克,超市決定把這兩種蘋果的售價提高x元,在不考慮其他因素的條件下,使超市銷售這兩種蘋果共獲利960元,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:拋物線與直線y=x+3分別交于x軸和y軸上同一點,交點分別是點A和點C,且拋物線的對稱軸為直線x=-2.
(1)求出拋物線與x軸的兩個交點A、B的坐標.
(2)試確定拋物線的解析式.
(3)觀察圖象,請直接寫出二次函數值小于一次函數值的自變量x的取值范圍.
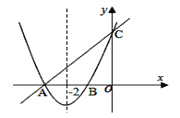
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解全校學生上學的交通方式,該校九年級(8)班的4名同學聯合設計了一份調查問卷,對該校部分學生進行了隨機調查.按A(騎自行車)、B(乘公交車)、C(步行)、D(乘私家車)、E(其他方式) 設置選項,要求被調查同學從中單選.并將調查結果繪制成條形統計圖1和扇形統計圖2,根據以上信息, 解答下列問題:
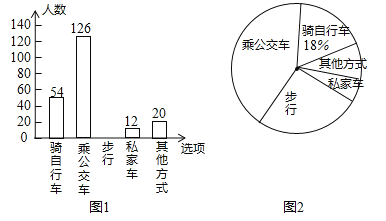
(1)本次接受調查的總人數是 人, 并把條形統計圖補充完整;
(2)在扇形統計圖中,“步行”的人數所占的百分比是 ,“其他方式”所在扇形的圓心角度數是 ;
(3)已知這4名同學中有2名女同學,要從中選兩名同學匯報調查結果.請你用列表法或畫樹狀圖的方法, 求出恰好選出1名男生和1名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在“愛護地球,綠化祖國”的活動中,組織同學開展植樹造林活動,為了了解全校同學的植樹情況,學校隨機抽查了一部分同學的植樹情況,將調查數據整理繪制成如下所示的統計圖.下面有四個推斷:![]() 這次調查獲取的樣本數據的樣本容量是100;
這次調查獲取的樣本數據的樣本容量是100;![]() 這次調查獲取的樣本數據的中位數是6棵;
這次調查獲取的樣本數據的中位數是6棵;![]() 這次調查獲取的樣本數據的眾數是4棵;
這次調查獲取的樣本數據的眾數是4棵;![]() 這次調查獲取的樣本數據的平均數是8棵.其中合理的是( )
這次調查獲取的樣本數據的平均數是8棵.其中合理的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為二次函數y=ax2+bx+c(a≠0)的圖象,則下列說法:①a>0 ②2a+b=0 ③a+b+c>0 ④當﹣1<x<3時,y>0,其中正確的個數為( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com