
已知一拋物線經過 (0,0),
(0,0), (1,1)兩點,且解析式的二次項系數為
(1,1)兩點,且解析式的二次項系數為
(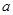 >0).
>0).
1.當 時,求該拋物線的解析式,并用配方法求出該拋物線的頂點坐標;
時,求該拋物線的解析式,并用配方法求出該拋物線的頂點坐標;
2.已知點 (0,1),若拋物線與射線
(0,1),若拋物線與射線 相交于點
相交于點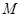 ,與
,與 軸相交于點
軸相交于點 (異于原點),當
(異于原點),當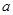 在什么范圍內取值時,
在什么范圍內取值時,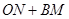 的值為常數?當
的值為常數?當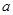 在什么范圍內取值時,
在什么范圍內取值時, 的值為常數?
的值為常數?
3.若點 (
( ,
, )在拋物線上,則稱點
)在拋物線上,則稱點 為拋物線的不動點.將這條拋物線進行平移,使其只有一個不動點,此時拋物線的頂點是否在直線
為拋物線的不動點.將這條拋物線進行平移,使其只有一個不動點,此時拋物線的頂點是否在直線 上,請說明理由.
上,請說明理由.
1.設該拋物線的解析式為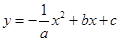 ,
,
∵拋物線經過(0,0)、(1,1)兩點,
∴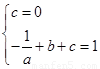 ,解得
,解得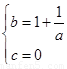 .
.
∴該拋物線的解析式為 ………………………………………1分
………………………………………1分
(Ⅰ)當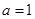 時,該拋物線的解析式為
時,該拋物線的解析式為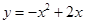 …………………………2分
…………………………2分
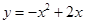
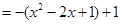
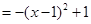 .
.
該拋物線的頂點坐標為(1,1) . ……………………………………3分
2.∵點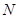 在
在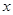 軸上,∴點
軸上,∴點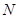 的縱坐標為0.
的縱坐標為0.
當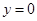 時,有
時,有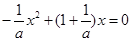 ,解得
,解得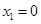 ,
,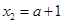 .
.
∵點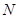 異于原點,∴點
異于原點,∴點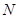 的坐標為(
的坐標為(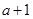 ,0).∴
,0).∴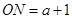 ………………4分
………………4分
∵點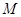 在射線
在射線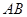 上,∴點
上,∴點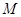 的縱坐標為1.
的縱坐標為1.
當 時,有
時,有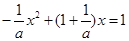 ,
,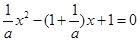 ,
,
解得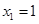 ,
,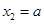 .
.
點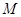 的坐標為(1,1)或(
的坐標為(1,1)或(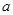 ,1)
. ……………………………5分
,1)
. ……………………………5分
當點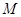 的坐標為(1,1)時,
的坐標為(1,1)時,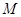 與
與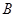 重合,此時
重合,此時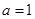 ,
,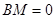 ,
,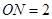 .
.
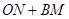 與
與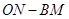 的值都是常數2.
的值都是常數2.
當點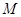 的坐標為(
的坐標為(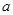 ,1)時,
,1)時,
若點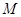 在點
在點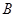 右側,此時
右側,此時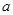 >1,
>1,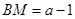 .
.
∴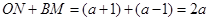 ,
,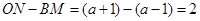 .
.
若點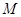 在點
在點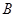 左側,此時0<
左側,此時0<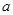 <1,
<1,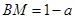 .
.
∴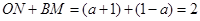 ,
,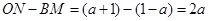 .
.
∴當0<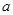 ≤1時,
≤1時,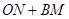 的值是常數2. ..………………………………6分
的值是常數2. ..………………………………6分
當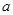 ≥1時,
≥1時,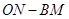 的值是常數2. ……………………………………7分
的值是常數2. ……………………………………7分
3.設平移后的拋物線的解析式為 ,
,
由不動點的定義,得方程: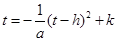 , ………………8分
, ………………8分
即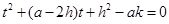 .
.
∵平移后的拋物線只有一個不動點,∴此方程有兩個相等的實數根.
∴判別式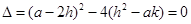 ,
.…………………9分
,
.…………………9分
有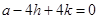 ,
,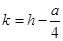 .
.
∴頂點(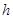 ,
,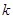 )在直線
)在直線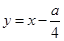 上. …………………………………10分
上. …………………………………10分
【解析】先用二次項系數為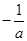 及O、B兩點坐標,
及O、B兩點坐標,
得出拋物線的解析式為
(I) 把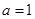 代入求得拋物線的解析式,然后利用拋物線圖象的性質求出頂點坐標;
代入求得拋物線的解析式,然后利用拋物線圖象的性質求出頂點坐標;
(II) 利用N點坐標在x軸上求出N點坐標,利用M點在直線AB上求出M點坐標,分別討論M點在B點兩側情況,從而得出ON+BM和ON-BM為常數的a取值范圍;
設平移后的拋物線的解析式為 ,利用不動點的定義,把P點坐標代入拋物線方程中,利用只有一個不動點,即是方程有兩個相等的實數根的性質得出h、k的關系,得出點(h,k)在直線
,利用不動點的定義,把P點坐標代入拋物線方程中,利用只有一個不動點,即是方程有兩個相等的實數根的性質得出h、k的關系,得出點(h,k)在直線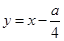 上.
上.


科目:初中數學 來源: 題型:
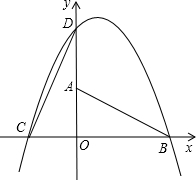 ,OB=4,現將Rt△AOB繞著直角頂點O按逆時針方向旋轉90°得到△COD,已知一拋物線經過C、D、B三點.
,OB=4,現將Rt△AOB繞著直角頂點O按逆時針方向旋轉90°得到△COD,已知一拋物線經過C、D、B三點.查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| a |
| a |
| 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (a>0).
(a>0). 上,請說明理由.
上,請說明理由.查看答案和解析>>
科目:初中數學 來源:2013年湖北省黃石九中中考數學模擬試卷(一)(解析版) 題型:解答題
 (a>0).
(a>0). 上,請說明理由.
上,請說明理由.查看答案和解析>>
科目:初中數學 來源:2012年天津市紅橋區中考數學二模試卷(解析版) 題型:解答題
 (a>0).
(a>0). 上,請說明理由.
上,請說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com