
【題目】如圖,在平面直角坐標(biāo)系中,矩形ABCD的頂點A、D在坐標(biāo)軸上,其坐標(biāo)分別為(2,0),(0,4),對角線AC⊥x軸. 
(1)求直線DC對應(yīng)的函數(shù)解析式
(2)若反比例函數(shù)y= ![]() (k>0)的圖象經(jīng)過DC的中點M,請判斷這個反比例函數(shù)的圖象是否經(jīng)過點B,并說明理由.
(k>0)的圖象經(jīng)過DC的中點M,請判斷這個反比例函數(shù)的圖象是否經(jīng)過點B,并說明理由.
【答案】
(1)解:如圖所示:過點D作DE⊥AC,垂足為E.

∵DE⊥AC,AC∥y軸,
∴∠EDO=90°.
∴∠EDA+∠ODA=90°.
又∵ABCD為矩形,
∴∠CDE+∠ADE=90°.
∴∠CDE=∠ODA.
又∵∠DOA=∠DEC=90°,
∴△DAO∽△DCE.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得EC=1.
,解得EC=1.
∴C(2,5).
設(shè)直線DC的解析式為y=kx+4,將點C的坐標(biāo)代入得:2k+4=5,解得k= ![]() .
.
∴直線CD的解析式為y= ![]() x+4
x+4
(2)解:過點D作DE⊥AC,過點B作BF⊥AC.

∵DE⊥AC,BF⊥AC.
∴∠DEC=∠BFA=90°.
∵DC∥AB,
∴∠DCE=∠FAB.
在△DEC和△BAF中  ,
,
∴△DEC≌△BAF.
∴DE=BF=2,EC=AF=1.
∴B(4,1).
∵D(0,4),C(2,5),
∴CD中點M的坐標(biāo)為(1, ![]() ).
).
∴k=1× ![]() =
= ![]() .
.
∵4×1=4≠ ![]() ,
,
∴點B不在反比例函數(shù)圖象上
【解析】過點D作DE⊥AC,垂足為E.先證明△DAO∽△DCE,依據(jù)相似三角形的性質(zhì)可求得EC=1,從而可求得EC的長,故此可得到點C的坐標(biāo),設(shè)直線DC的解析式為y=kx+4,將點C的坐標(biāo)代入求解即可;(2)過點D作DE⊥AC,過點B作BF⊥AC.先證明△DEC≌△BAF,從而可求得點B的坐標(biāo),然后再求得反比例反函數(shù)比例系數(shù)k的值,然后根據(jù)點B的坐標(biāo)是否符合函數(shù)解析式進行判斷即可.
【考點精析】通過靈活運用確定一次函數(shù)的表達式和矩形的性質(zhì),掌握確定一個一次函數(shù),需要確定一次函數(shù)定義式y(tǒng)=kx+b(k不等于0)中的常數(shù)k和b.解這類問題的一般方法是待定系數(shù)法;矩形的四個角都是直角,矩形的對角線相等即可以解答此題.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知數(shù)軸上點A表示的數(shù)為8,B是數(shù)軸上一點,且AB=14.
![]()
(1)寫出數(shù)軸上點B表示的數(shù);
(2)若點M、N分別是線段AO、BO的中點,求線段MN的長;
(3)若動點P從點A出發(fā).以每秒5個單位長度的速度沿數(shù)軸向左勻速運動,動點Q從點B出發(fā),以每秒3個單位長度的速度沿數(shù)軸向左勻速運動,若點P、Q同時出發(fā).問點P運動多少秒時追上點Q?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為順利通過“國家文明城市”驗收,東營市政府?dāng)M對城區(qū)部分路段的人行道地磚、綠化帶、排水管道等公用設(shè)施全面更新改造,根據(jù)市政建設(shè)的需要,需在40天內(nèi)完成工程.現(xiàn)有甲、乙兩個工程隊有意承包這項工程,經(jīng)調(diào)查知道,乙工程隊單獨完成此項工程的時間是甲工程隊單獨完成此項工程時間的2倍,若甲、乙兩工程隊合作只需10天完成.
(1)甲、乙兩個工程隊單獨完成此項工程各需多少天?
(2)若甲工程隊每天的工程費用是4.5萬元,乙工程隊每天的工程費用是2.5萬元,請你設(shè)計一種方案,既能按時完工,又能使工程費用最少.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于x的一元二次方程x2+(m-2)x+m+1=0有兩個相等的實數(shù)根,則m的
值是
A. 0 B. 8 C. 4±2![]() D. 0或8
D. 0或8
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖.AB是⊙O的直徑,E為弦AP上一點,過點E作EC⊥AB于點C,延長CE至點F,連接FP,使∠FPE=∠FEP,CF交⊙O于點D. 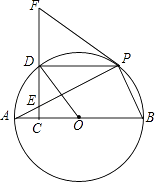
(1)證明:FP是⊙O的切線;
(2)若四邊形OBPD是菱形,證明:FD=ED.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A,B,與y軸交于點C,其中點A在y軸的左側(cè),點C在x軸的下方,且OA=OC=5.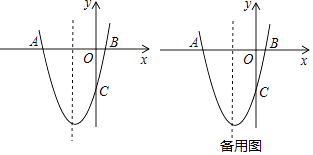
(1)求拋物線對應(yīng)的函數(shù)解析式;
(2)點P為拋物線對稱軸上的一動點,當(dāng)PB+PC的值最小時,求點P的坐標(biāo);
(3)在(2)條件下,點E為拋物線的對稱軸上的動點,點F為拋物線上的動點,以點P、E、F為頂點作四邊形PEFM,當(dāng)四邊形PEFM為正方形時,請直接寫出坐標(biāo)為整數(shù)的點M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點A、B在數(shù)軸上分別表示實數(shù)![]() 、
、![]() ,A、B兩點之間的距離記作AB.
,A、B兩點之間的距離記作AB.
當(dāng)A、B兩點中有一點為原點時,不妨設(shè)A點在原點.如圖①所示,則AB=OB=![]() =
=![]() .
.
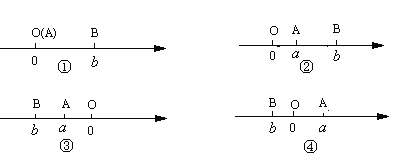
當(dāng)A、B兩點都不在原點時:
(1)如圖②所示,點A、B都在原點的右邊,不妨設(shè)點A在點B的左側(cè),則AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(2)如圖③所示,點A、B都在原點的左邊,不妨設(shè)點A在點B的右側(cè),則AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(3)如圖④所示,點A、B分別在原點的兩邊,不妨設(shè)點A在點O的右側(cè),則AB=OB+OA=![]() =
=![]() =
=![]()
回答下列問題:
(1)綜上所述,數(shù)軸上A、B兩點之間的距離AB= .
(2)數(shù)軸上表示2和-4的兩點A和B之間的距離AB= .
(3)數(shù)軸上表示![]() 和-2的兩點A和B之間的距離AB= ,如果AB=2,則
和-2的兩點A和B之間的距離AB= ,如果AB=2,則![]() 的值為 .
的值為 .
(4)若代數(shù)式![]() 有最小值,則最小值為 .
有最小值,則最小值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=2 ![]() ,AD=4,點E是BC邊上一個動點,連接AE,作DF⊥AE于點F,當(dāng)BE的長為時,△CDF是等腰三角形.
,AD=4,點E是BC邊上一個動點,連接AE,作DF⊥AE于點F,當(dāng)BE的長為時,△CDF是等腰三角形. 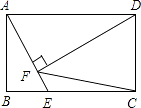
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
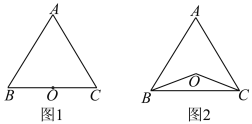
【題目】已知點O到△ABC的兩邊AB,AC所在直線的距離相等,且OB=OC.
(1)如圖1,若點O在邊BC上,求證:∠ABC=∠ACB;
(2)如圖2,若點O在△ABC的內(nèi)部,則∠ABC=∠ACB成立嗎?并說明理由;
(3)若點O在△ABC的外部,則∠ABC=∠ACB成立嗎?請畫圖表示.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com