
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經過A(﹣1,0),B(4,0),C(0,2)三點. 
(1)求這條拋物線的解析式;
(2)E為拋物線上一動點,是否存在點E,使以A、B、E為頂點的三角形與△COB相似?若存在,試求出點E的坐標;若不存在,請說明理由;
(3)若將直線BC平移,使其經過點A,且與拋物線相交于點D,連接BD,試求出∠BDA的度數.
【答案】
(1)解:∵該拋物線過點C(0,2),
∴可設該拋物線的解析式為y=ax2+bx+2.
將A(﹣1,0),B(4,0)代入,
得 ![]() ,
,
解得 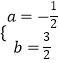 ,
,
∴拋物線的解析式為:y=﹣ ![]() x2+
x2+ ![]() x+2.
x+2.
(2)解:存在.
由圖象可知,以A、B為直角頂點的△ABE不存在,所以△ABE只可能是以點E為直角頂點的三角形.
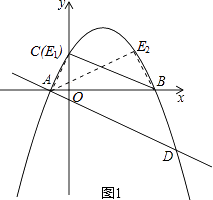
在Rt△BOC中,OC=2,OB=4,
∴BC= ![]() =2
=2 ![]() .
.
在Rt△BOC中,設BC邊上的高為h,則 ![]() ×2
×2 ![]() h=
h= ![]() ×2×4,
×2×4,
∴h= ![]() .
.
∵△BEA∽△COB,設E點坐標為(x,y),
∴ ![]() =
= ![]() ,
,
∴y=±2
將y=2代入拋物線y=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
得x1=0,x2=3.
當y=﹣2時,不合題意舍去.
∴E點坐標為(0,2),(3,2).
(3)解:如圖2,連結AC,作DE⊥x軸于點E,作BF⊥AD于點F,
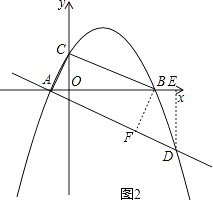
∴∠BED=∠BFD=∠AFB=90°.
設BC的解析式為y=kx+b,由圖象,得
![]() ,
,
∴  ,
,
yBC=﹣ ![]() x+2.
x+2.
由BC∥AD,設AD的解析式為y=﹣ ![]() x+n,由圖象,得
x+n,由圖象,得
0=﹣ ![]() ×(﹣1)+n
×(﹣1)+n
∴n=﹣ ![]() ,
,
yAD=﹣ ![]() x﹣
x﹣ ![]() .
.
∴﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() x﹣
x﹣ ![]() ,
,
解得:x1=﹣1,x2=5
∴D(﹣1,0)與A重合,舍去;
∴D(5,﹣3).
∵DE⊥x軸,
∴DE=3,OE=5.
由勾股定理,得BD= ![]() .
.
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2.
∴AB=5
在Rt△AOC中,Rt△BOC中,由勾股定理,得
AC= ![]() ,BC=2
,BC=2 ![]() ,
,
∴AC2=5,BC2=20,AB2=25,
∴AC2+BC2=AB2
∴△ACB是直角三角形,
∴∠ACB=90°.
∵BC∥AD,
∴∠CAF+∠ACB=180°,
∴∠CAF=90°.
∴∠CAF=∠ACB=∠AFB=90°,
∴四邊形ACBF是矩形,
∴AC=BF= ![]() ,
,
在Rt△BFD中,由勾股定理,
得DF= ![]() ,
,
∴DF=BF,
∴∠ADB=45°.
【解析】(1)本題需先根據已知條件,過C點,設出該拋物線的解析式為y=ax2+bx+2,再根據過A,B兩點,即可得出結果;(2)由圖象可知,以A、B為直角頂點的△ABE不存在,所以△ABE只可能是以點E為直角頂點的三角形.由相似關系求出點E的坐標;(3)如圖2,連結AC,作DE⊥x軸于點E,作BF⊥AD于點F,由BC∥AD設BC的解析式為y=kx+b,設AD的解析式為y=kx+n,由待定系數法求出一次函數的解析式,就可以求出點D坐標,由勾股定理就可以求出BD的值,由勾股定理的逆定理就可以得出∠ACB=90°,由平行線的性質就可以得出∠CAD=90°,就可以得出四邊形ACBF是矩形,就可以得出BF的值,由勾股定理求出DF的值,而得出DF=BF而得出結論.
【考點精析】解答此題的關鍵在于理解等腰直角三角形的相關知識,掌握等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°,以及對矩形的性質的理解,了解矩形的四個角都是直角,矩形的對角線相等.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
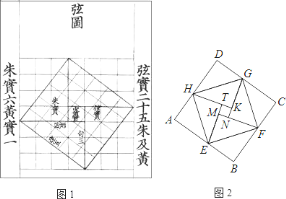
【題目】漢代數學家趙爽為了證明勾股定理,創制了一幅“弦圖”,后人稱其為“趙爽弦圖”(如圖![]() ).圖
).圖![]() 是由弦圖變化得到的,它由八個全等的直角三角形拼接而成,記圖中正方形
是由弦圖變化得到的,它由八個全等的直角三角形拼接而成,記圖中正方形![]() 、正方形
、正方形![]() 、正方形
、正方形![]() 的面積分別為
的面積分別為![]() 、
、![]() 、
、![]() .若
.若![]() ,則
,則![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的兩點OA、OC分別在x軸、y軸的正半軸上,點G為矩形對角線的交點,經過點G的雙曲線y= ![]() 在第一象限的圖象與BC相交于點M,交AB于N,若已知S△MBN=9,則k的值為 .
在第一象限的圖象與BC相交于點M,交AB于N,若已知S△MBN=9,則k的值為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一個四邊形紙片ABCD,∠B=∠D=90°,把紙片按如圖所示折疊,使點B落在AD邊上的B'點,AE是折痕。

(1)試判斷B'E與DC的位置關系并說明理由。
(2)如果∠C=130°,求∠AEB的度數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,E為矩形ABCD邊AD上一點,點P從點B沿折線BE﹣ED﹣DC運動到點C時停止,點Q從點B沿BC運動到點C時停止,它們運動的速度都是1cm/s.若點P,Q同時開始運動,設運動時間為t(s),△BPQ的面積為y(cm2).已知y與t的函數關系圖象如圖2,有下列四個結論:①AE=6cm;②sin∠EBC= ![]() ;③當0<t≤10時,y=
;③當0<t≤10時,y= ![]() t2; ④當t=12s時,△PBQ是等腰三角形.其中正確結論的序號是 .
t2; ④當t=12s時,△PBQ是等腰三角形.其中正確結論的序號是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,△OAB如圖放置,點A的坐標為(3,4),點P是AB邊上的一點,過點P的反比例函數 ![]() 與OA邊交于點E,連接OP.
與OA邊交于點E,連接OP.
(1)如圖1,若點B的坐標為(5,0),且△OPB的面積為 ![]() ,求反比例函數的解析式;
,求反比例函數的解析式;
(2)如圖2,過P作PC∥OA,與OB交于點C,若 ![]() ,并且△OPC的面積為
,并且△OPC的面積為 ![]() ,求OE的長.
,求OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的高,AE、BF分別是∠BAC、∠ABC的平分線,∠BAC=50°,∠ABC=60°,則∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com