
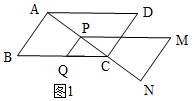
【題目】如圖1所示,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射線AC的方向勻速平移得到△PNM,速度為1cm/s,同時,點Q從點C出發,沿射線CB方向勻速運動,速度為1cm/s,當△PNM停止平移時,點Q也停止運動,如圖2所示,設運動時間為t(s)(0<t<4).
(1)當t為何值時,PQ∥MN?
(2)設△QMC的面積為y(cm2),求y與t之間的函數關系式;
(3)是否存在某一時刻t,使得PQ=QM,若存在,求出t的值;若不存在,請說明理由.
【答案】
(1)
解:如圖1,由題意得:CQ=AP=t,
在Rt△ABC中,由勾股定理得AC= ![]() =
= ![]() =4,
=4,
∴CP=4﹣t,
由平移的性質可得MN∥AB,
∵PQ∥MN,
∴PQ∥AB,
∴ ![]() ,即
,即 ![]() ,
,
解得t= ![]() ,
,
則當t為何值時,PQ∥MN
(2)
解:如圖2,過點P作PF⊥BC于點F,過點A作AE⊥BC于點E,
由S△ABC= ![]() AB×AC=
AB×AC= ![]() AE×BC,
AE×BC,
![]() ×3×4=
×3×4= ![]() ×5AE,
×5AE,
可得:AE= ![]() ,
,
則由勾股定理易得:CE= ![]() =
= ![]() =
= ![]() .
.
∵PD⊥BC,AE⊥BC,
∴AE∥PD,
∴△CPD∽△CAE,
∴ ![]() ,即
,即 ![]()
∴PD= ![]() ,CD=
,CD= ![]() ,
,
∵PM∥BC,
∴點M到BC的距離h=PD= ![]() ,
,
∴△QCM的面積y= ![]() CQ×h=
CQ×h= ![]() ×
× ![]() =﹣
=﹣ ![]() +
+ ![]() (0<t<4)
(0<t<4)

(3)
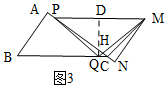
解:如圖3,過點Q作QD⊥PM于點D,QD交AC于點H.
∵PQ=MQ,
∴PD=DM= ![]() ,且DQ⊥BC.
,且DQ⊥BC.
在Rt△ABC中,AC=4,AP=t,QC=t.
∵∠A=∠HQC,∠ACB=∠QCH,
∴△CQH∽△CAB,
∴ ![]() ,即
,即 ![]() ,
,
∴CH= ![]() t,
t,
∴PH=AC﹣AP﹣CH=4﹣t﹣ ![]() t=4﹣
t=4﹣ ![]() t,
t,
易證△PHD∽△CBA,
∴ ![]() ,
,
即 ![]() ,
,
解得t= ![]() .
.
∴當t= ![]() 時,PQ=QM.
時,PQ=QM.
【解析】(1)如圖1,先根據題意得:CQ=AP=t,利用勾股定理求AC的長,根據PQ∥AB,列比例式可求得t的值;(2)如圖2,作輔助線,構建相似三角形,利用面積法得:S△ABC= ![]() AB×AC=
AB×AC= ![]() AE×BC,可得:AE=
AE×BC,可得:AE= ![]() ,由勾股定理易得:CE=
,由勾股定理易得:CE= ![]() .證明△CPD∽△CAE,列比例式
.證明△CPD∽△CAE,列比例式 ![]() ,求PD和CD的長,根據面積公式求△QCM的面積y;(3)如圖3,作輔助線,構建相似三角形,證明△CQH∽△CAB,列比例式得:
,求PD和CD的長,根據面積公式求△QCM的面積y;(3)如圖3,作輔助線,構建相似三角形,證明△CQH∽△CAB,列比例式得: ![]() ,表示CH=
,表示CH= ![]() t,則PH=AC﹣AP﹣CH=4﹣
t,則PH=AC﹣AP﹣CH=4﹣ ![]() t,易證△PHD∽△CBA,列式可求得t的值.
t,易證△PHD∽△CBA,列式可求得t的值.
【考點精析】利用勾股定理的概念和平行四邊形的性質對題目進行判斷即可得到答案,需要熟知直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】有三張正面分別標有數字﹣3,1,3的不透明卡片,它們除數字外都相同,現將它們背面朝上,洗勻后從三張卡片中隨機地抽取一張,放回卡片洗勻后,再從三張卡片中隨機地抽取一張.
(1)試用列表或畫樹狀圖的方法,求兩次抽取的卡片上的數字之積為負數的概率;
(2)求兩次抽取的卡片上的數字之和為非負數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,∠BAC的平分線AD交⊙O于點D,過點D垂直于AC的直線交AC的延長線于點E. 
(1)求證:DE是⊙O的切線;
(2)如果AD=5,AE=4,求AC長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在不透明的布袋中裝有1個白球,2個紅球,它們除顏色外其余完全相同.
(1)從袋中任意摸出兩個球,試用樹狀圖或表格列出所有等可能的結果,并求摸出的球恰好是兩個紅球的概率;
(2)若在布袋中再添加x個白球,充分攪勻,從中摸出一個球,使摸到白球的概率為 ![]() ,求添加的白球個數x.
,求添加的白球個數x.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請從以下兩個小題中任選一個作答,若多選,則按所選的第一小題計分.
①若單項式﹣xmyn+4 與 5x2y 是同類項,則 nm 的值為____.
②實施西部大開發戰略是黨中央的重大決策,我國國土面積約為960 萬平方千米,而我國西部地區的面積占我國國土面積的 ![]() ,用科學記數法表示我國西部地區的面積約為_____平方千米.
,用科學記數法表示我國西部地區的面積約為_____平方千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:課外興趣小組活動時,老師提出了如下問題:
如圖1,△ABC中,若AB=5,AC=3,求BC邊上的中線AD的取值范圍.
小明在組內經過合作交流,得到了如下的解決方法:延長AD到E,使得DE=AD,再連接BE(或將△ACD繞點D逆時針旋轉180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三邊關系可得2<AE<8,則1<AD<4.
感悟:解題時,條件中若出現“中點”“中線”字樣,可以考慮構造以中點為對稱中心的中心對稱圖形,把分散的已知條件和所求證的結論集中到同一個三角形中.
(1)問題解決:受到(1)的啟發,請你證明下面命題:如圖2,在△ABC中,D是BC邊上的中點,DE⊥DF,DE交AB于點E,DF交AC于點F,連接EF.
①求證:BE+CF>EF;②若∠A=90°,探索線段BE、CF、EF之間的等量關系,并加以證明;
(2)問題拓展:如圖3,在平行四邊形ABCD中,AD=2AB,F是AD的中點,作CE⊥AB,垂足E在線段AB上,聯結EF、CF,那么下列結論①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序號).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序號).


圖1 圖2 圖3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個三角形內有n個點,在這些點及三角形頂點之間用線段連接起來,使得這些線段互不相交,且又能把原三角形分割為不重疊的小三角形.如圖:若三角形內有1個點時此時有3個小三角形;若三角形內有2個點時,此時有5個小三角形.則當三角形內有3個點時,此時有個小三角形;當三角形內有n個點時,此時有個小三角形.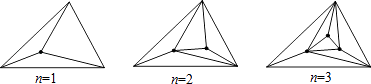
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,O是AC上一動點(不與點A、C重合),過O作直線MN∥BC,設MN交∠BCA的平分線于點E,交∠BCA的外角平分線于點F.
(1)OE與OF相等嗎?證明你的結論;
(2)試確定點O的位置,使四邊形AECF是矩形,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個3×3的方格中填寫了9個數字,使得每行、每列、每條對角線上的三個數之和相等,得到的3×3的方格稱為一個三階幻方.
(1)在圖1中空格處填上合適的數字,使它構成一個三階幻方;
(2)如圖2的方格中填寫了一些數和字母,當x+y的值為多少時,它能構成一個三階幻方.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com