
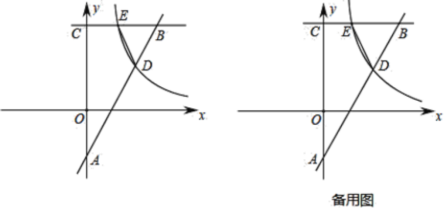
【題目】Rt△OBC在直角坐標系內的位置如圖所示,點C在y軸上,∠OCB=90°,反比例函數y=![]() (k>0)在第一象限內的圖象與OB邊交于點D(m,3),與BC邊交于點E(n,6).
(k>0)在第一象限內的圖象與OB邊交于點D(m,3),與BC邊交于點E(n,6).
(1)求m與n的數量關系;
(2)連接CD,若△BCD的面積為12,求反比例函數的解析式和直線OB的解析式;
(3)設點P是線段OB邊上的點,在(2)的條件下,是否存在點P,使得以B、C、P為項點的三角形與△BDE相似?若存在,求出此時點P戶的坐標;若不存在,請說明理由.
【答案】(1)m=2n;(2)直線OB的解析式![]() ,反比例函數的解析式
,反比例函數的解析式![]() ;(3)點P的坐標為(4,2);
;(3)點P的坐標為(4,2);
【解析】
(1)根據點在反比例函數圖像上得到方程,即可得到結論;
(2)如圖,過點D作DF⊥BC于點F,可得DF=3,根據三角形的面積公式可得BC=8,即可得到結論;
(3)如圖,作PG⊥BC于G,①當△BED∽△BCP時,②當△BED∽△BPC時,根據相似三角形的判定和性質即可得到結論.
(1)∵點D(m,3)與E(n,6)在y=![]() (k>0)上
(k>0)上
∴![]()
∴m與n的數量關系為m=2n;
(2)如圖,過點D作DF⊥BC于點F,可得DF=3,
∴![]()
解得BC=12,
∴B點坐標(12,6)
∴直線OB的解析式![]() ;
;
∵點D(m,3)在OB邊上
∴D點坐標(6,3)
∴反比例函數的解析式![]() ;
;
(3)如圖,作PG⊥BC于G,由(2)得E點坐標(3,6)
①當△BED∽△BCP時,∠BED=∠BCP,![]() =
=![]() ,
,
∴DF⊥BC,PG⊥BC,
∴DF∥PG,
∴△BDF∽△BPG,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() ,
,
∴PG=4,
∴P(4,2);
②當△BED∽△BPC時,![]() =
=![]() ,
,
∴![]() ,
,
∴BP=![]() ,
,
∵![]() =
=![]() ,即
,即 .
.
∴PG=7.2![]() ,此時P不在線段OB上,
,此時P不在線段OB上,
綜上所述,點P的坐標為(4,2).


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在矩形紙片ABCD中,AB=3cm,AD=5cm,折疊紙片使B點落在邊AD上的E處,折痕為PQ,過點E作EF∥AB交PQ于F,連接BF.
(1)求證:四邊形BFEP為菱形;
(2)當點E在AD邊上移動時,折痕的端點P、Q也隨之移動;
①當點Q與點C重合時(如圖2),求菱形BFEP的邊長;
②若限定P、Q分別在邊BA、BC上移動,求出點E在邊AD上移動的最大距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
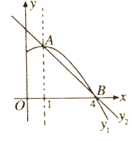
【題目】如圖是拋物線![]() 圖象的一部分,拋物線的頂點是
圖象的一部分,拋物線的頂點是![]() ,對稱軸是直線
,對稱軸是直線![]() ,且拋物線與
,且拋物線與![]() 軸的一個交點為
軸的一個交點為![]() ;直線
;直線![]() 的解析式為
的解析式為![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③方程
;③方程![]() 有兩個不相等的實數根;④拋物線與
有兩個不相等的實數根;④拋物線與![]() 軸的另一個交點是
軸的另一個交點是![]() ;⑤當
;⑤當![]() 時,則
時,則![]() .其中正確的是( )
.其中正確的是( )
A.①②B.①③⑤C.①④D.①④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,AC是半圓內一條弦,點D是![]() 的中點,DB交AC于點G,過點A作半圓的切線與BD的延長線交于點M,連接AD.點E是AB上的一動點,DE與AC相交于點F.
的中點,DB交AC于點G,過點A作半圓的切線與BD的延長線交于點M,連接AD.點E是AB上的一動點,DE與AC相交于點F.
(1)求證:MD=GD;
(2)填空:①當∠DEA= 時,AF=FG;
②若∠ABD=30°,當∠DEA= 時,四邊形DEBC是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
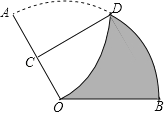
【題目】如圖,一張扇形紙片OAB,∠AOB=120°,OA=6,將這張扇形紙片折疊,使點A與點O重合,折痕為CD,則圖中未重疊部分(即陰影部分)的面積為( )
A.9![]() B.12π﹣9
B.12π﹣9![]() C.
C.![]() D.6π﹣
D.6π﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
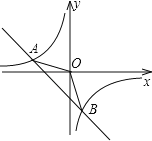
【題目】如圖,已知A(﹣4,n),B(2,﹣4)是一次函數y=kx+b和反比例函數y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求一次函數和反比例函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
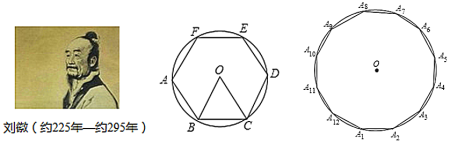
【題目】劉徽計算圓周率是從正六邊形開始的,易知圓的內接正六邊形可分為六個全等的正三角形,每個三角形的邊長均為圓的半徑![]() .此時圓內接正六邊形的周長為
.此時圓內接正六邊形的周長為![]() ,如果將圓內接正六邊形的周長等同于圓的周長,可得圓周率為3.當正十二邊形內接于圓時,如果按照上述方法計算,可得圓周率為______.(參考數據:
,如果將圓內接正六邊形的周長等同于圓的周長,可得圓周率為3.當正十二邊形內接于圓時,如果按照上述方法計算,可得圓周率為______.(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代重要建筑的室內上方,通常會在正中部位做出向上凸起的穹窿狀裝飾,稱為藻井.北京故宮博物院內的太和殿上方即有藻井(圖1),全稱為龍鳳角蟬云龍隨瓣枋套方八角渾金蟠龍藻井.它展示出精美的裝飾空間和造型藝術.從分層構造上來看,太和殿藻井由三層組成:最下層為方井,中層為八角井,上層為圓井.圖2是由圖1抽象出的平面圖形.若最下層方井邊長為1,在圖2中隨機取一點,則此點取自圓內的概率為( )

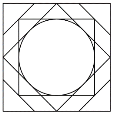
圖1 圖2
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com