Question

　　(常德市2003年中考試題)二次函數y=ax²+Bx+c的圖象如圖所示，那么關于此二次函數的下列四個結論：①a＜0；②c＞0；③B²-4ac＞0；④＜0中，正確的結論有    (　)

　　A．1個　　　　　　　　　　　　 B．2個

　　C．3個　　　　　　　　　　　　 D．4個

 

Answer 1

答案：D
解析：

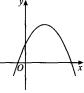
解析：根據拋物線y=ax2+Bx+c的圖象與a、B、c的關系，可以判定出結果． 　　∵　拋物線的開口向下，∴　a＜0．又∵　對稱軸在y軸的右側，∴　a、B異號．∴　＜0．又∵　拋物線與y軸的交點在y軸的正半軸上，∴　c＞0．由拋物線與x軸有兩個交點，得B2-4ac＞0.∴　①②③④都正確． 　　點評：本題體現了數形結合法的應用，這是解決函數問題極為重要的數學方法．能借助函數的圖象來研究函數的性質． 　　對于拋物線y=ax2+Bx+c有以下特點： 　　(1)a的符號由開口方向確定：開口向上，a＞0；開口向下，a＜0．簡記作“上正下負”． 　　(2)B的符號由對稱軸的位置和a的符號共同確定：對稱軸在y軸的左側，a、B同號；對稱軸在y軸的右側，a、B異號；對稱軸在y軸上，B=0．簡記作“左同右異，在y軸B=0”． 　　(3)c的符號由拋物線與y軸交點的位置確定：拋物線與y軸的交點在y軸的正半軸，c＞0；拋物線與y軸的交點在y軸的負半軸，c＜0；拋物線與y軸的交點在原點，c=0．簡記作“上正下負，過原點c=0”． 　　(4)B2-4ac的符號由拋物線x軸交點的個數確定：拋物線與x軸有2個交點，B2-4ac＞0；拋物線與x軸有1個交點，B2-4ac=0；拋物線與x軸沒有交點，則B2-4ac＜0．簡記作“二正一零沒有負”． 　　(5)a+B+c的符號由拋物線上橫坐標為1的點的位置確定：拋物線上橫坐標為1的點在x軸上方，a+B+c＞0；拋物線上橫坐標為1的點在x軸的下方，a+B+c＜0；拋物線上橫坐標為1的點在x軸上，a+B+c=0．簡記作“上正下負，在x軸上等于0”． 　　(6)a-B+c的符號由拋物線上橫坐標為-1的點的位置確定：拋物線上橫坐標為-1的點在x軸的上方，a-B+c＞0；拋物線上橫坐標為-1的點在x軸的下方，a-B+c＜0；拋物線上橫坐標為-1的點在x軸上，a-B+c=0．簡記作“上正下負，在x軸上等于0”．