
【題目】(1)解方程:x2﹣2x﹣3=0;
(2)如圖,正方形ABCD中,點E,F,C分別在AB,BC,CD上,且∠EFG=90°;求證:△EBF∽△FCG.

科目:初中數學 來源: 題型:
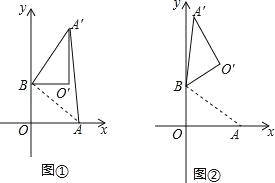
【題目】在平面直角坐標系中,O 為原點,點 A(4,0),點 B(0,3),把△ABO 繞點 B 逆時針旋轉,得△A′BO′,點 A、O 旋轉后的對應點為 A′、O′,記旋轉角為ɑ.
(1)如圖 1,若ɑ=90°,求 AA′的長;
(2)如圖 2,若ɑ=120°,求點 O′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的袋子中裝有三個完全相同的小球,分別標有數字2,3,4.從袋子中隨機取出一個小球,用小球上的數字作為十位數字,然后放回,再取出一個小球,用小球上的數字作為個位數字,這樣組成一個兩位數,請用列表法或畫樹狀圖的方法完成下列問題.
(1)按這種方法組成兩位數45是_____事件,填(“不可能”、“隨機”、“必然”)
(2)組成的兩位數能被3整除的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自行車因其便捷環保深受人們喜愛,成為日常短途代步與健身運動首選.如圖1是某品牌自行車的實物圖,圖2是它的簡化示意圖.經測量,車輪的直徑為66cm,車座B到地面的距離BE為90cm,中軸軸心C到地面的距離CF為33cm,車架中立管BC的長為60cm,后輪切地面L于點D.(參考數據:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
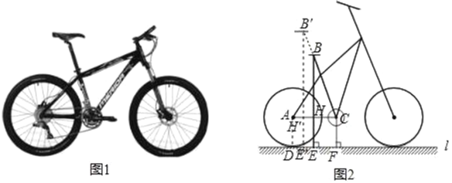
(1)求∠ACB的大小(精確到1°)
(2)如果希望車座B到地面的距離B'E′為96.8cm,車架中立管BC拉長的長度BB′應是多少?(結果取整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
如圖,拋物線y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,直線l經過B、C兩點,點M從點A出發以每秒1個單位長度的速度向終點B運動,連接CM,將線段MC繞點M順時針旋轉90°得到線段MD,連接CD、BD.設點M運動的時間為t(t>0),請解答下列問題:
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,直線l經過B、C兩點,點M從點A出發以每秒1個單位長度的速度向終點B運動,連接CM,將線段MC繞點M順時針旋轉90°得到線段MD,連接CD、BD.設點M運動的時間為t(t>0),請解答下列問題:

(1)求點A的坐標與直線l的表達式;
(2)①請直接寫出點D的坐標(用含t的式子表示),并求點D落在直線l上時t的值;
②求點M運動的過程中線段CD長度的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
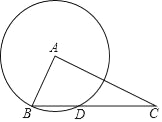
【題目】如圖,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A為圓心、AB為半徑畫圓,與邊BC交于另一點D.
,以A為圓心、AB為半徑畫圓,與邊BC交于另一點D.
(1)求BD的長;
(2)連接AD,求∠DAC的正弦值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() (其中
(其中![]() 、
、![]() 為常數且
為常數且![]() )與
)與![]() 軸交于
軸交于![]() 和
和![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)當![]() 時,求拋物線的對稱軸方程及頂點坐標;
時,求拋物線的對稱軸方程及頂點坐標;
(2)填空:![]() __________,點
__________,點![]() 的坐標為____________.(以上結果均用含
的坐標為____________.(以上結果均用含![]() 的式子表示);
的式子表示);
(3)連接![]() ,線段
,線段![]() 的垂直平分線交拋物線的對稱軸于點
的垂直平分線交拋物線的對稱軸于點![]() ,
,![]() 軸上存在一點
軸上存在一點![]() (異于點
(異于點![]() )使得
)使得![]() .
.
①求點![]() 的坐標;
的坐標;
②點![]() 關于拋物線對稱軸的對稱點為點
關于拋物線對稱軸的對稱點為點![]() ,試求
,試求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=ax2﹣2ax﹣3(a≠0)與x軸交于A,B兩點(點A在點B左側).

(1)求拋物線的對稱軸;
(2)若AB=4,求該拋物線的解析式;
(3)若AB≤4,直接寫出a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com